我們可能一天到晚聽到:FB 又改了它的演算法啦~ 這個技術背後的演算法邏輯是Blahblah阿~
一直演算法演算法,聽起來好像很厲害… 但它到底是什麼意思呢?!是一種技術嗎?是一種數學嗎?到底演算法又和程式有什麼差異呢?
今天就要來帶大家看看什麼是演算法(Algorithm),在本文內甚至可以教大家針對一個問題、寫出相對應的演算法,在未來看到這個詞別再害怕噢~
- 在觀看本文之前的推薦影音(記得開中文字幕噢!):
什麼是演算法?
演算法是用以解決特定問題的有限個步驟和敘述。
在電腦尚未問世以前,演算法就是數學家極為重要的研究主題。現在也是電腦科學中非常重要的基礎科目。
演算法並非程式語言,而是一種思考流程。程式語言代表的則是符合該語言的文法規則;所以我們可以先把解決問題的流程寫下來、再把這個程式碼轉換成相應的程式語言。
比如相同的問題和解決流程、程式碼可以寫成 C/C++、Python、Java…。
也就是說,我們會先有演算法,再把演算法轉換成程式。
一般來說,演算法須滿足下列五個標準:
1. 輸入(Input):輸入的資料量至少(大於等於) 0 個。
2. 輸出(Output):輸出的結果至少(大於等於)1 個。
3. 明確性(Definiteness):演算法中的每一個敘述都必須是明確的定義。
註:比如「天氣冷的時候穿上外套」,就不具備明確性。因為每個人對於天氣冷會有不同的看法。「天氣溫度為攝氏 10 度的時候穿上外套」就具備明確性。
4. 有限性(Finiteness):演算法必須在執行有限個步驟後能夠終止。也就是說不能無限期的執行。
註:但程式(Program)不一定要滿足有限個。
(1) 比如 infinite loop recursion(無限遞迴的程式)。雖然你的電腦會一直跑一直跑跑到爆炸、永遠不會停,但這個程式還是可以跑噢!
int a = 5;
while (a > 0){
a++; /* 只要符合 a > 0 ,即不斷將 a+1 */
}
(2) 為了實際上的必要:
作業系統在不關機的情況下要能不斷的跑;或是保全系統亦然(可以說這個保全系統程式跑一遍就夠了嗎ˊ__>ˋ)。
5. 有效性(Effectiveness):演算法中的每個敘述必須是夠基本,可讓人用紙和筆即可追蹤。這是一個操作型的定義。
註:如果要解決一個問題,要先想好問題、再去找一個程式語言把它寫下來的話,會很沒有效率。
比如說程式真正在跑的時候不work,我們要怎麼知道到底是解法有問題,還是轉換成程式的時候寫錯,還是Compile的時候出錯?可能有問題的地方太多,還要花時間寫好程式才能對答案的話也太過耗時。
第五點的重點是要驗證「問題解法的有效性」。不用考慮效能和程式語言的語法,只要用紙筆即能 trace 完演算法、確定問題能解。工程師在寫程式的時候就能更快地確定是哪邊出了差錯。
不過另外要注意的是,正確性(Correctness)並不在演算法的五個標準之內。因為我們的「有效性」標準是要「可操作」,就是能用紙筆Run一次。就算演算法出了差錯、那也還叫演算法。
如何想出並表達一個演算法?
演算法最大的挑戰,在於如何想出問題的解法。瞭解演算法也就是瞭解問題如何被解決的過程。
想出演算法的能力不見得可以透過學習提升,很多時候會需要像藝術創作一樣的靈感…ˊ__>ˋ。要想出好的演算法,大致上的流程是:
1. 分析問題(有無輸入資料?條件限制?)
2. 想出解決問題的辦法(雖然這看起來有點廢話,不過主要是去思考:有沒有類似問題已經有解法?如果還想不到,可以縮小問題的範圍,看看到什麼程度可以想出解法,再擴大它。)
3. 擬定演算法的步驟、再轉換成相對應的程式。
4. 評估該演算法是否具備能用來解決其他類似問題的潛力。
要構思出演算法,我們可以運用一些容易理解的方式,將思考流程表達出來。其實就是把你自己當作一台電腦,想想看你會如何依序解決一個問題呢?
讓我們舉個例子好了,比如:找出 {23, 5, 33, 7, 82} 這幾個數字中的最大值。如果你是電腦,會怎麼做呢?
你可能會這麼做:
- 先將最大值的初始值設為 0 。
- 如果最大值和 23 比較、發現 23 大,就把 23 設為最大值。(此時最大值被改成 23)
- 如果最大值和 5 比較、發現 5 大,就把 5 設為最大值。(此時最大值仍為 23)
- 如果最大值和 33 比較、發現 33 大,就把 33 設為最大值。(此時最大值為 33)
- 如果最大值和 7 比較、發現 7 大,就把 7 設為最大值。(此時最大值仍為 33)
- 如果最大值和 82 比較、發現 82 大,就把 82 設為最大值。(此時最大值為 82)
- 將最大值的結果印出來。
哇!事實上你已經寫完一個演算法了呢!
如果將上面的過程用程式語言(範例為 C 語言)寫下來,就會是:
int main(){
int max = 0; /* 將最大值的初始值設為 0 */
if (23 > max) /* 若23較大,就把最大值設為23 */
max = 23;
if (5 > max) /* 若5較大,就把最大值設為5 */
max = 5;
if (33 > max) /* 若33較大,就把最大值設為33 */
max = 33;
if (7 > max) /* 若7較大,就把最大值設為7 */
max = 7;
if (82 > max) /* 若82較大,就把最大值設為8 */
max = 82;
printf("最大值為 %d", max); /* 印出最大值 */
}
當然,用這種做法的缺點就是程式沒有擴充性——如果改變要比較的數值、或數值的個數,整個程式就必須重寫。
所以根據相同的演算法,我們可以換一種程式的寫法:
int main(){
int i;
/* 宣告一個變數i */
int list[5] ={23, 5, 33, 7, 82};
/* 將5個整數存放在一個陣列中 */
int max = 0;
/* 將最大值的初始值設為0 */
for (i = 0; i < 5; i++){
/* 在這個陣列中的第1到第5個元素中(i等於1~5) */
if (list[i] > max)
/* 如果第i個元素值大於最大值 */
max = list[i];
/* 將最大值設為第i個元素的值 */
}
printf("最大值為 %d", max);
/* 印出最大值 */
}
一旦要比較的數值或個數被改變,只要改掉第 3 行的陣列大小和元素、並將第 5 行的 i 改成新的個數即可。相較前一個程式、如此寫法更具備擴充性。
然而注意到了嗎,我們解決問題的方法其實是一樣的!只是程式的寫法不同了而已。也就是說在演算法的階段,只是要「想出解決問題的流程」而已。
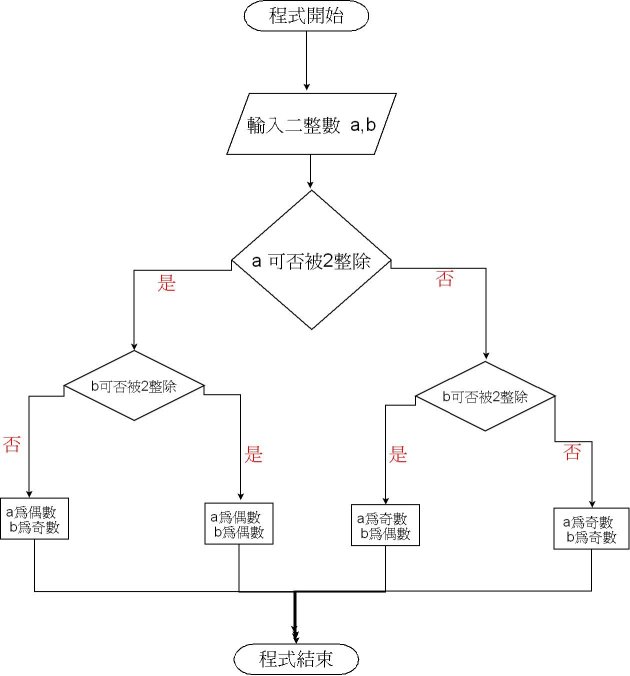
演算法的常見表達的方式,包括了「流程圖」(Flowchart)或「虛擬碼」(Pseudocode)。
上述即為使用流程圖,來判斷兩個數字為奇數或偶數的演算法。
另一種更常見的表達方式是虛擬碼(Pseudocode)。通常是一般的口語敘述,來描述問題的解法。這樣的虛擬碼並不能實際作為一個程式跑起來。
像是我們在上面一步步寫下來「比大小」解決問題流程,就是一個虛擬碼噢!
當然讀者可能會發現,如果不是用程式碼、而是用描述的方式寫下來,那寫法就可以有很多種呀!
像是如果我想把它寫成更接近程式碼的樣貌,就可以寫成:
1. 先將最大值的初始值設為 0
2. while (如果有很多個數值){
if (現在比較的數值>最大值)
then 將最大值設為現在的數值
end if
end while
}
3. print (結果)
這樣也是一個演算法的虛擬碼噢!虛擬碼並不是真的要在電腦上執行,所以只要能看得懂就行了、沒有什麼語法要遵守。
你可以把「 a 這個變數的值是 5 」的這句話寫成:
- a = 5; (把 5 這個值 assign 給 a)
- a <- 5; (把 a 的值設定為 5)
- a is 5;
也由於沒有固定的語法,因此大部分人傾向採用將來想要撰寫程式的程式語言(比如這個問題之後打算要用 C 還是 Python 解),來作為虛擬碼。
那既然同一個解決流程、可以有不同種演算法的寫法,那到底要怎麼知道哪一種方法比較好呢?這就牽涉到效能分析的問題啦!
演算法的效能分析
既然針對同一個問題所撰寫的演算法有許多種,要判斷優劣、我們會依據下列兩方面來分析:
1. 空間複雜度(Space Complexity):執行完畢所需的記憶體空間。
2. 時間複雜度(Time Complexity):執行完畢所需的時間。
其中,時間複雜度又比空間複雜度更重要。一來是因為現在的儲存空間很便宜;二來是資料量變大時,空間複雜度的差異通常不大、但時間複雜度則會有極大的差異。
所以一般來說,我們會專注於討論時間複雜度。
再進一步來說,由於多數程式還有編譯、運行環境的差異,因此我們通常會討論演算法的時間複雜度時,而非程式。
那我們要如何測量執行時間呢?通常是計算每執行一次有幾個步驟(Steps per Execution)。也就是統計演算法中、要執行步驟的次數加總。
這種測量結果和電腦的執行速度沒關係,但和輸入(Input)、輸出(Output)資料量習習相關。如果想要計算的資料越多,時間複雜度也就越高。
比如下列程式【計算 n 個數的總和】的步驟數如下:
- S/E (Steps per Execution):該敘述每執行一次、需要花費多少個步驟
- 頻率 (Frequency):該敘述的執行次數。
- 程式的步驟數 (Total):S/E * 頻率。
int program(int n){
int i, sum;
sum = 0;
/* S/E = 1, 頻率 = 1, Total = 1 */
for (i = 1; i <= n; i++){
/* S/E = 3, 頻率 = n+1, Total = 3(n+1) */
sum = sum + i;
/* S/E = 1, 頻率 = n, Total = n */
}
return sum;
/* S/E = 1, 頻率 = 1, Total = 1 */
}
把 Total 加起來:1 + 3(n+1) + n + 1 = 4n+5,即這個演算法的時間需求。
其實對於電腦來說,由於電腦的執行速度很快,所以對於時間複雜度的係數和常數(比如 4n+5 的 4 和 5)在資料量很大很大的時候,都可以省略,只針對次方的部份討論。
也就是將 4n+5 、300n+1234 等,全都視為與 n 相同的線性關係。但 4n² + 5,則視為 n²。
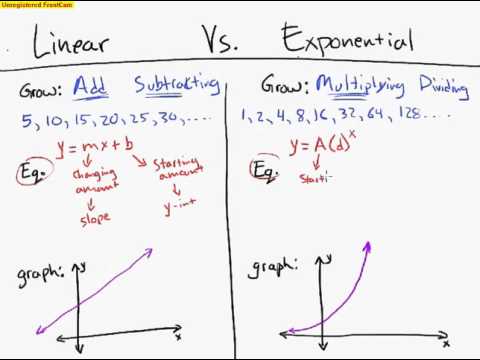
也就是說,我們在意的是時間複雜度的成長速度(Growth Rate)是線性成長、還是指數型成長。
不知道大家有沒有聽過一個故事——有個大臣因功向國王邀賞,獎賞內容是要求國王將第一個棋盤格子中擺 1 粒稻米、第二個棋盤格子中擺 2 粒稻米、第三個格子中擺 4 粒… 以此類推到 101 個格子。
國王表示:安安,這個要求太容易了!差點就要答應下來,直到被身邊的一位智者阻止。答案會變成 2 的 100 次方,也就是 2676506 * 10 的 30 次方的驚人天文數字。挖空全國的稻米都不知道給不給得出來。
由此可知,線性成長、和指數型成長的速度差異,是非常巨大的!所以我們要尋求一種方法,來描述執行時間相對於問題大小的成長速度。
這種方法,就是規範出理論的上限值–– 符號表達為「O」,唸作 Big-Oh。
理論上,這支演算法的成長速度會小於這個上限值,也就是說在最差的情況下,表現也不會比 O( )差。比如【計算 n 個數的總和】的時間複雜度即 O(4n+5) = O(n)。
舉例來說,若有兩支功能相同的演算法(都能解決同樣一個問題),但時間複雜度卻分別為 O(n) 與 O(n²)。現在讓它們各自在一部每秒鐘能執行 100 個指令的電腦上、處理 100 萬筆資料,各需花費多少時間呢?
答案是:O(n) 只需 1 秒鐘,然而 O(n²) 則需要 100 萬秒。因此若是一個演算法的時間複雜度高達 O(n²) 時,通常都會想辦法縮減。
演算法是一門能夠動動腦的有趣科目,也是要解決很實際的問題。未來將會陸續出接下來的幾集給初學者,歡迎大家繼續收看噢!
(不過還是建議要有一些程式基礎再來看~若沒學過程式的讀者看完這篇就可以了,之後請先存起來吧XDD)