本文是《一看就懂的 IC》系列第六集。接續一看就懂的 一看就懂的 IC 產業結構與競爭關係,《一看就懂的IC》系列將持續為大家介紹 IC 與硬體的核心基礎概念。
為什麼說電腦是只有 0 和 1 的世界?如何用電路來實現運算呢?為什麼要說邏輯電路、邏輯運算、邏輯晶片呢?(那個「邏輯」到底代表什麼意思?)
世界上只有 10 種人,一種是懂二進位的、一種是不懂二進位的。看完這篇文章,保證通通搞懂以上問題、對科技產業的最最最基本名詞有點概念吧!
二進制運算
從這邊開始,我們要來討論一個很重要的問題──既然電腦是一台計算機,計算機為什麼能夠「計算」?它不就只是一堆電路串在一起嗎?要達到一台機器能夠「計算」,需要有哪些條件呢?
關於這個問題,我們可以進一步將問題拆解成三個想法去解決它:
(1) 數字在計算機中該如何表示?
電路有辦法表示人類認知中的正整數、小數,甚至是負數等等數字嗎?如果連該如何在電路中表示數字都不知道,更別提要進一步做運算了。
(2) 數字在計算機中如何運算?
找到了表示數字的方法後,接下來看看該如何利用電路來進行運算。要怎麼做加法,甚至是減法、乘法、除法呢?也是按照人類計算的方法運算嗎?
(3) 如何用電路實現?
知道數字該如何表示與運算的方法後,要怎麼實作出一個真能運算的電路呢?
好啦,接下來讓我們一一來討論吧!
(1) 數字在計算機中該如何表示?
常聽到一句話:「電腦是只有 0 和 1 的世界」。「0」和「1」到底是什麼意思呢?
與其說是數字,不如稱作兩個相對的狀態,比如「ON」、「OFF」的電燈開關。
想像一台計算機零件的電路上佈滿了電線、每條電線都有著兩種狀態的電壓──當超過一定的電壓 (閥值) 時、稱為「H」(高位準),低於則稱為「L」(低位準)。或說成「電流有無流通」的 ON、OFF 都行,也就是具備了 2 個狀態的電子零件。
為了要表示「L」和「H」兩個狀態,我們使用了「0」與「1」來表達;這裡的 0、1 並不是真正的數值,而只是象徵符號而已。
你想用「○」、「●」或「陰」、「陽」來表達;或是把「H」定義為「0」、「L」定義為「1」也行。總之就是兩個相對狀態的符號。
很顯然地,和製造具備 2 個狀態的電子零件相比,要製造出具有 3 個狀態以上的電子零件,工藝上會更加困難(因為一條電線上的電壓,自然就是有高電壓和低電壓相對兩種電壓),因此我們選擇用前者來造計算機。
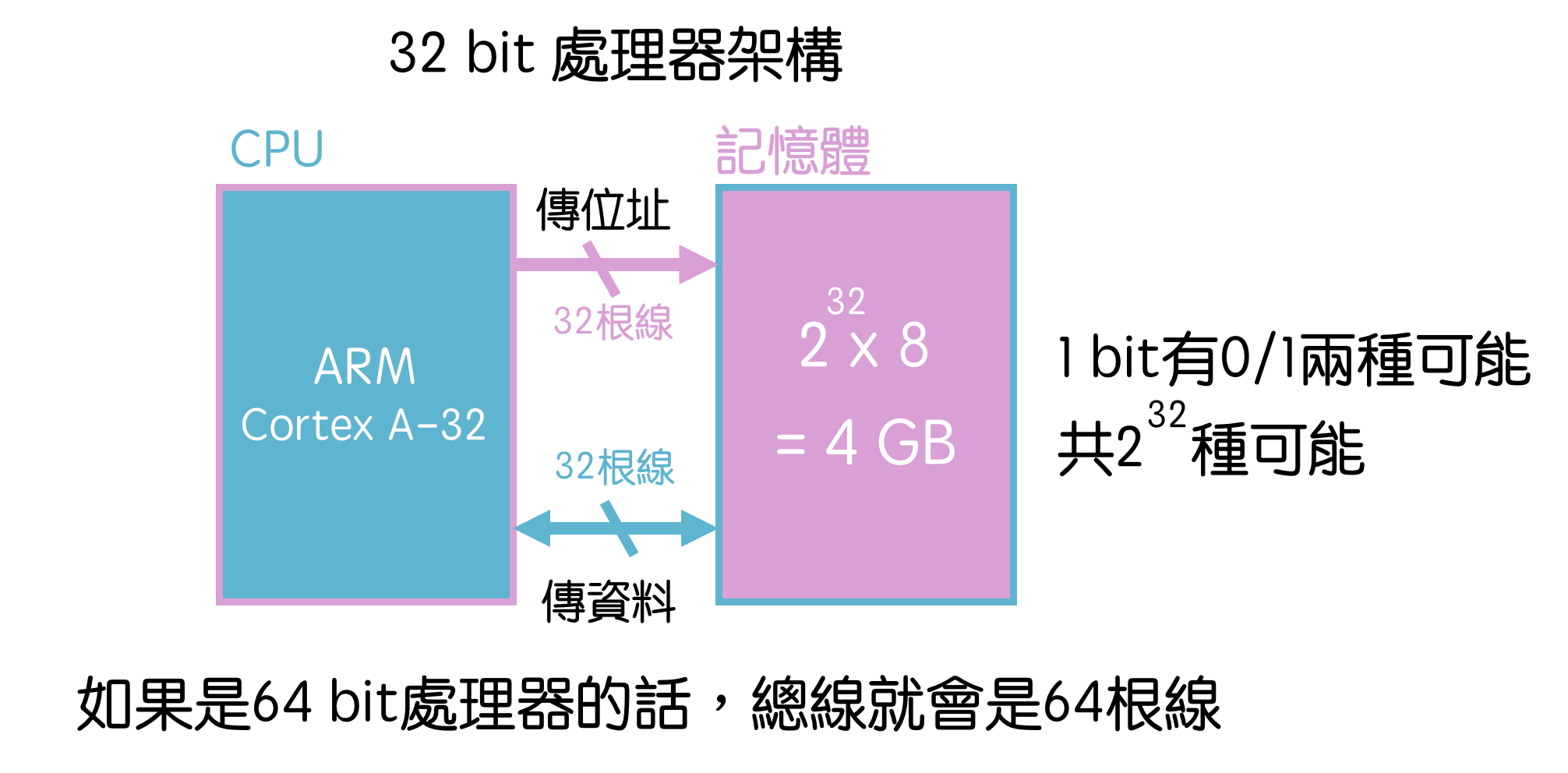
一天到晚聽到「你的電腦是 32 位元處理器還是 64 位元處理器 」這個問題嗎?其實就是根據 CPU 的架構,有 32 bit 或 64 bit 數量的匯流排 (Bus)。
讓我們回到記憶體——還記得我們說過記憶體就是一個大倉庫、由一堆格子組成的嗎?那這些格子有多大呢?
8 bit 會等於 1 byte;一般會用小寫 b 代表bit、大寫 B 代表 byte。目前所有記憶體的格子容量都是 1 byte(8 bit)的大小。
想要知道倉庫有多大,除了得知道一個格子多大,還得知道格子有幾個?想像我們在這些格子上面拉電路線、每條線都有「通電」和「不通電」(或高電壓、低電壓)兩種選擇,也就是「1」和「0」。
由於有 32 條線、每條線有兩種可能,就可以組成 2^32 種地址。每個地址的格子容量都是 1 byte,等於記憶體容量是 【2^32(為 4 Giga) * 1 byte(8 bit)】 = 【4GB】。也就是 4 Giga byte。
64 位元處理器,就是把匯流排從 32 根線變成 64 根線,資料傳輸容量會變得更大。
既然我們都是用電線上的 0 和 1 來表示,在運算時、故也勢必只能使用這兩個數字而已,也就是「二進位制」。
不過這並不代表要儲存資訊的話,都得用二進位噢!電腦之所以會採用二進位,只是因為好建構出來電路計算機。
想想看,如果我們不用電路,而是改用 DNA 來儲存資料、當作造記憶體或硬碟的技術,還會用二進位嗎?
什麼,用 DNA 當硬碟?
沒錯!DNA 其實是一種優良的儲存介質——用DNA儲存資料的優勢是 DNA 可以保存數千年之久,不會像CD 或錄影帶一樣過一陣子會消磁,而且 DNA 可以堆疊儲存、能帶來更高的儲存量。
近年來用 DNA 來作為儲存介質的呼聲很高,微軟甚至還有一個專案在負責研究開發 DNA 硬碟。DNA 硬碟在做的事,就是把 0 和 1 的資料轉換為 4 種核苷酸 ATCG。
但如果要這樣儲存的話,你可以考慮採用四進制,比如 DNA 的鹼基 ATCG,可以使用 00 代表 A、01 代表 C、10 代表G 、11 代表 T。
不過也有人後來表示說若用四進位,當連續的鹼基出現,比如 TTTTTTTT 時,就會導致偵測讀取的時候出問題。
如果直接以四進位編碼成DNA,會出現連續同樣的鹼基對,導致讀取出錯。所以有研究人員又提出了一種改良的方法叫「旋轉編碼」(Rotating Code):
簡單來說,就是上一個鹼基如果是 A,那麼下一個鹼基只能是 C、G、T,其中 C 代表0,G 代表1,T 代表 2;如果上一個是 C,下一個只能是 G、T、A,其中 G 代表0,T 代表 1,A 代表 2,以此類推。
以這種方式進行編碼,任意一個鹼基和前後的鹼基都是不一樣的。但是這樣一來,就只能同時使用四種鹼基中的三種來表示狀態,也就是最多只能用三進位。
好啦我們扯遠了。其實 Lynn 在此處要表達的意思只是——在不同的世界觀(或許糖果星人採用 7 進位制)、或不同的應用中,都是根據最理想解決問題的辦法,來決定你要採用什麼進位方法。別再以為世界上只有十進位啦!
對此直接下個結論就是:我們要用「0」和「1」來表示數字,和做計算與儲存資料,也就是「二進位制」運算。(這樣最簡單啦)
等等,那這個二進制到底是什麼意思呢?
講個笑話,如果看得懂的讀者就可以省略本文這段介紹了——「世界上可以分成 10 種人,懂二進位的人,以及不懂二進位的人。」
上圖擷取自一位PTT鄉民的簽名檔。呃… 究竟是誰才被做成簽名檔、被大家笑的那位呢…
如果您看不懂的話別緊張!這是因為你還只是人類世界的人,我們在人類世界的幼稚園和小學時期,也得學十進位的加減乘除和小數點。
既然你想要進入數位資訊的世界,勢必也要重新開始學習數位世界的數字是怎麼表達的~讓我們當自己是剛移民過來的外星物種,從數位世界的小學開始學起吧!
(不要告訴我說你想移民火星,卻連要學當地的數字表達方法都不肯吧!)
先讓我們來想想看平常人類習慣的「十進位」是怎麼運算的:
因為遇到十就會進一位,所以 6 是 10 的 零次方、 20 是 2 乘上 10 的一次方、400 是 4 乘上 10 的二次方。
利用這樣的思考方式,讓我們來看看什麼是「二進位數」:
若把二進位數的「1101」換成十進位數,就是「8 + 4 + 0 + 1 = 13」。
以上就是整數是如何在二進位數中被表達的。
所以什麼叫做「世界上只有 10 種人,一種懂二進位、一種不懂」呢?意思就是「 1 乘 2 的 1 次方 + 0 乘 2 的 0 次方 = 2」
這個 10 不是用十進位、而是用二進位去解讀的。
既然如此,那浮點數(小數點)該怎麼辦呢?讓我們再回過頭來想十進位的「小數點」是怎麼運算的:
「1.01」是 1 乘 10 的零次方、0 乘 10 的 -1 次方、1 乘 10 得 -2 次方的加總。
所以二進位的「1.01」呢?換過來講就是 1 乘 2 的零次方、0 乘 2 的 -1 次方、1 乘 2 的 -2 次方的加總。也就是我們十進位中的「5/4」。很簡單吧!
等等,那還有負數呢?電腦該如何表示一個數是正數、還是負數?
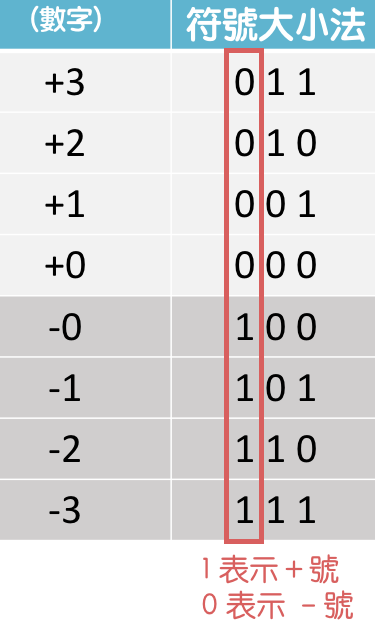
最簡單的辦法就是在數字的最左邊留用一個數字來表示正負數。
比如 1 表示此數為正、0 表示此數為負。這種表示法稱為「符號大小法」( Sign and Magnitude)。
想想看,如果只有這樣表示的話,會發生什麼樣的問題呢?
比如說:這個用來當符號的數字是要擺在最左邊還最右邊?還有, 「0」不就有「+ 0」和「- 0」 兩種表示了嗎?如果程式設計人員稍微粗心一點,就很容易發生錯誤。
要解決這問題有個辦法,就是取「補數」。
蛤?
想想看在十進位數中 「40 + (-40)」 和 「40 + (60)」的結果,分別為「00」和「100」。
若只看後兩位數,40 + (-40) 和 40 + (60) 的計算結果是不是一樣的?
因為在二個位數的計算上,不用管超過二個位數的數字,所以多出來的 1 就當作沒看到,這在電腦科學上稱為溢位 (Overflow)。
而 40 和 -60 的關係,我們可以稱之為「60 是 40 相對於 100 的補數」。也就是說,「和一個數字相加、會讓該數字產生溢位(進位)的數」就是「補數」。
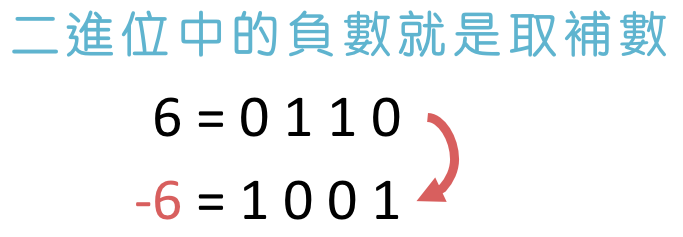
對於二進位數來說,由於只有 0 和 1,要做補數,就是把所有數字都反轉;比如把數字中的 0 都改成 1、1 都改成 0 就可以了。而這個補數,就相當於原數字的負數。
比如要表達「6」這個數字,就是把「0110」(6 的二進位數)取補數、變成「1001」。「1001」就代表「-6」了!
這種表示負數的方法和「符號大小法」不同,稱為「1’s 補數法」。
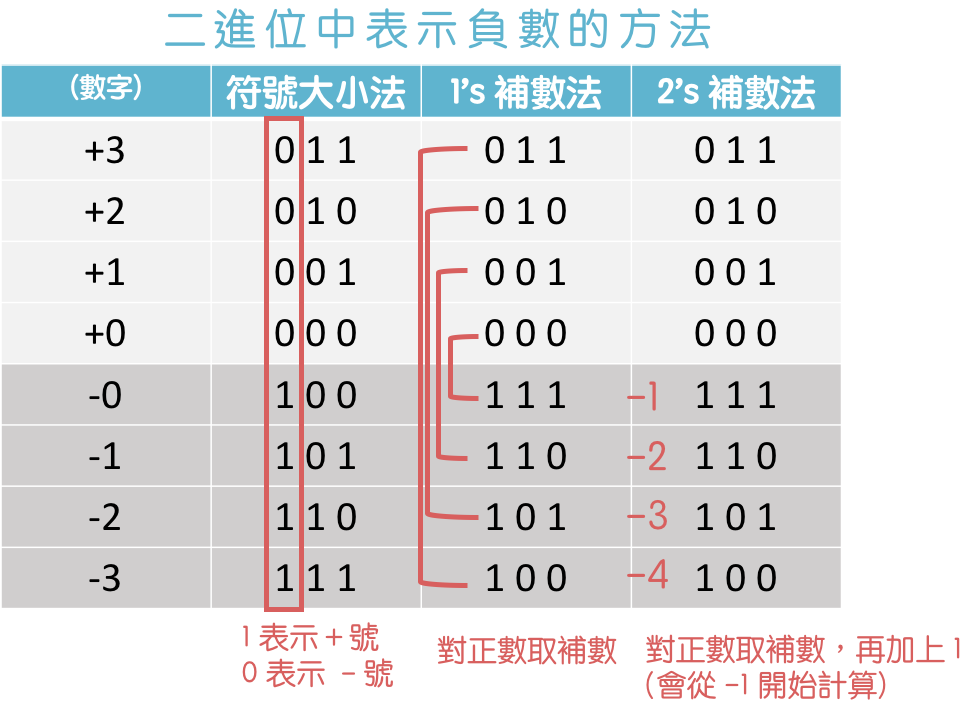
等等,但這樣 0 如果是「000」、取補數 -0 就會是「111」,還是沒有解決 0 有 +0 和 -0 兩種結果的問題啊?(000 和 111 都代表 0 也太奇怪了吧~)
為了改善,所以我們進一步再將數字加上 1 做修正。這種對「1’s 補數法」的進一步修正,我們稱為「2’s 補數法」。這樣要表示 0 的話,就只有 000 一種寫法了;負數會從 -1 開始計算。
比較一下這三種都能表示正負數的方法,不管哪一種、對正數的表示方法都是一樣的;不同的地方在於對負數地表示法。
由於「2’s 補數法」沒有「符號大小法」與「1’s 補數法」的缺點,所以現在的電腦全都是採用「2’s 補數法」來表示負數。
我們已經成功學會正數、小數點和負數的二進位表示法了!恭喜你從數位世界的小學畢業啦~~
笑話說:「世界上只有 10 種人,一種懂二進位、一種不懂」從現在開始,大家都是懂二進位的人了!
(2) 數字在計算機中如何運算?
既然我們已經知道在計算機中表達數字要用二進位數,那麼又該如何用二進位數做加減乘除的運算呢?和十進位數的做法是一樣的嗎?
當然不是!
一位著名的英國數學家布林(Boolean)在 1854 年發表了兩篇論文,奠定一種新型的學科基礎——「布林代數」,至今仍然是電腦科學領域的基本學科,為計算機的電路設計提供了理論基礎。(整死一堆唸電資科系的學生…被黑特的程度可能也是和牛頓/萊布尼茲發明微積分有得比)
那麼在布林代數中的運算,是不是也和十進制一樣的四則運算呢?非也,布林代數用的是「邏輯運算」推導,IC 電路使用的就是用布林代數原理做的「邏輯電路」。
(= =)?什麼是邏輯運算?
回答這個問題之前,首先、我們要對 IC 的內部構造有些基本認識:
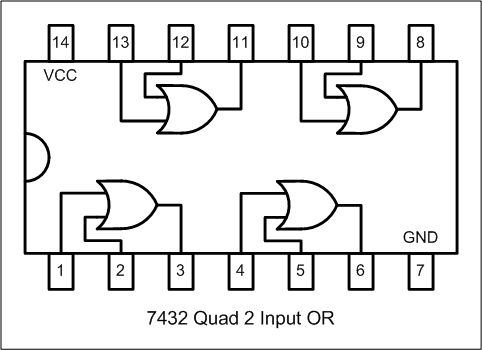
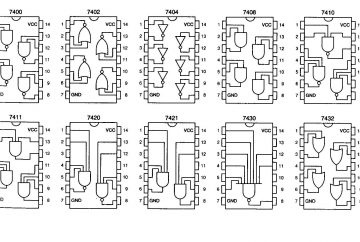
翻開由德州儀器開發的 TTL 74 系列 7432 晶片電路圖,可以看到中間用記號表示的邏輯電路,且每個記號都連接到 IC 的接腳(PIN)。
什麼是 IC 的接腳(Pin)?IC 晶片上會有許多接腳,能輸入和輸出數位訊號。
所以上面電路圖中每個有標數字的地方,都是一個接腳噢!(再重申一次,這張圖就是 IC 晶片內部的電路圖!!!)
好啦,讓我們來看看電路圖上的符號代表什麼意思吧!
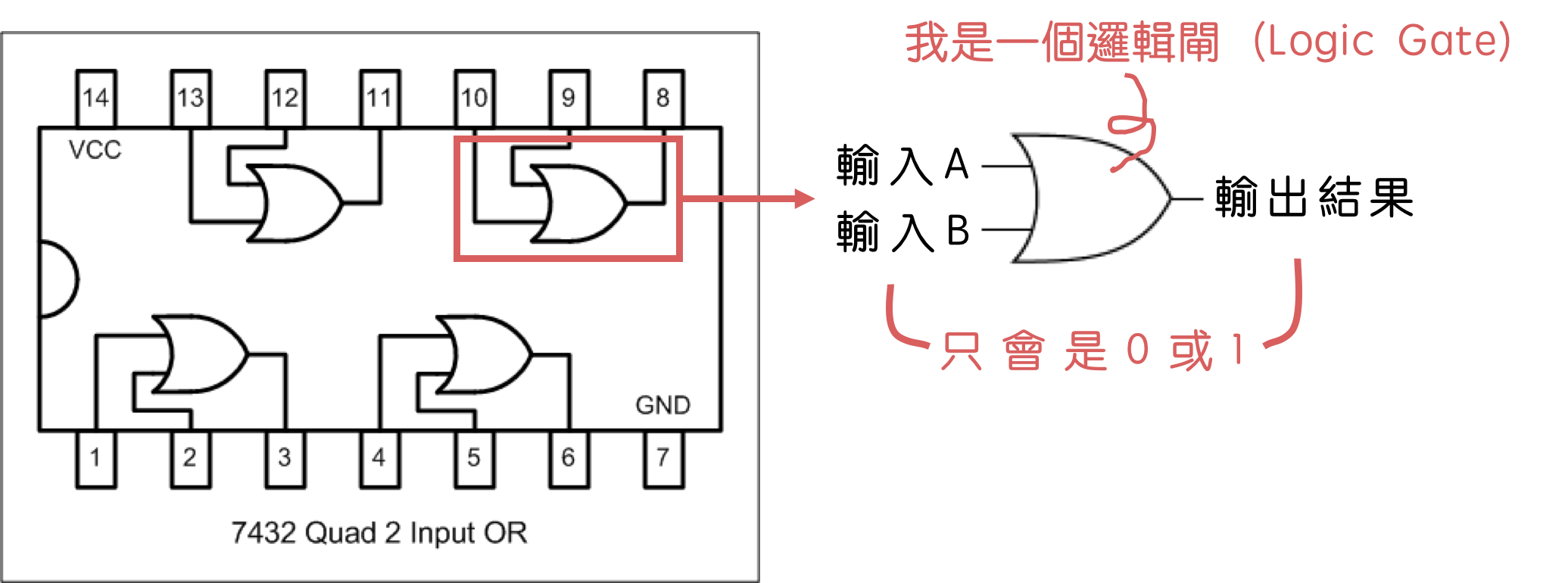
將電路圖上的符號拉出來看,可以發現是由兩個輸入、和一個輸出所組成。中間經過的閘(Gate)可以當成一個由電路構成的黑盒子,經過這個電路後、就可以輸出結果。
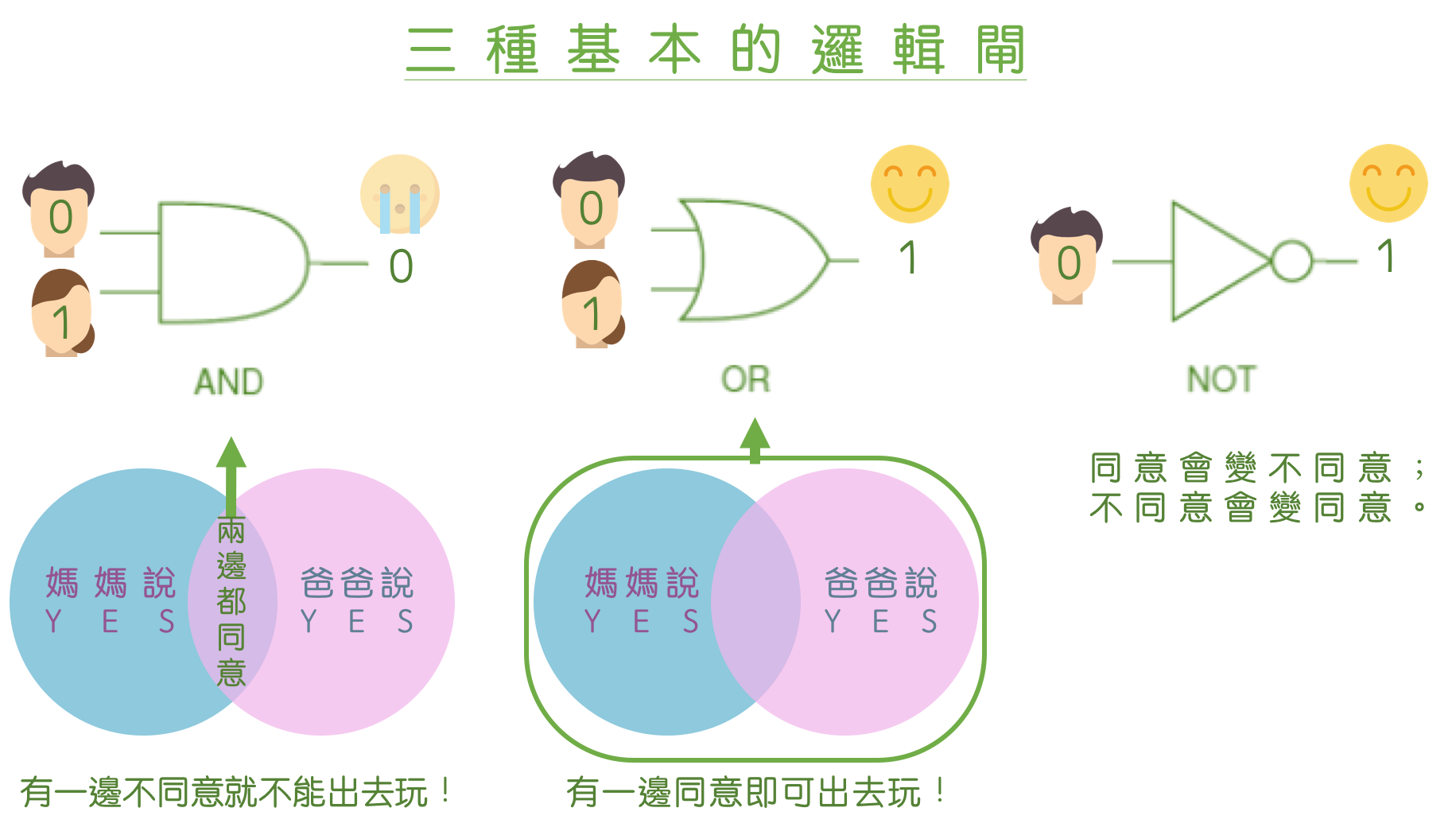
根據布林邏輯,可以做出三大基本的邏輯電路——「AND」、「OR」、「NOT」。每個電路都有兩個輸入、一個輸出結果。
要理解這些邏輯電路很簡單,想像成「問爸媽意見的過程」就行了:
- AND 電路:老爸和老媽都說 yes 才能出去玩、只要有一個說不准就不行。
- OR 電路:老爸或老媽至少一個人說 yes 就能出去玩。
- NOT 電路:小孩叛逆期,爸媽說 yes 會聽成 no、說 no 會聽成 yes。
yes 代表 1、no 代表 0,配合文氏圖的輔助,可以一眼看出三大基本電路的功能。
或是更明確一些,使用真值表把所有可能列出來:
再回去看一次 7432 電路圖,我們可以發現原來它就是由四個 OR 電路組成的呢!是不是很簡單呢~
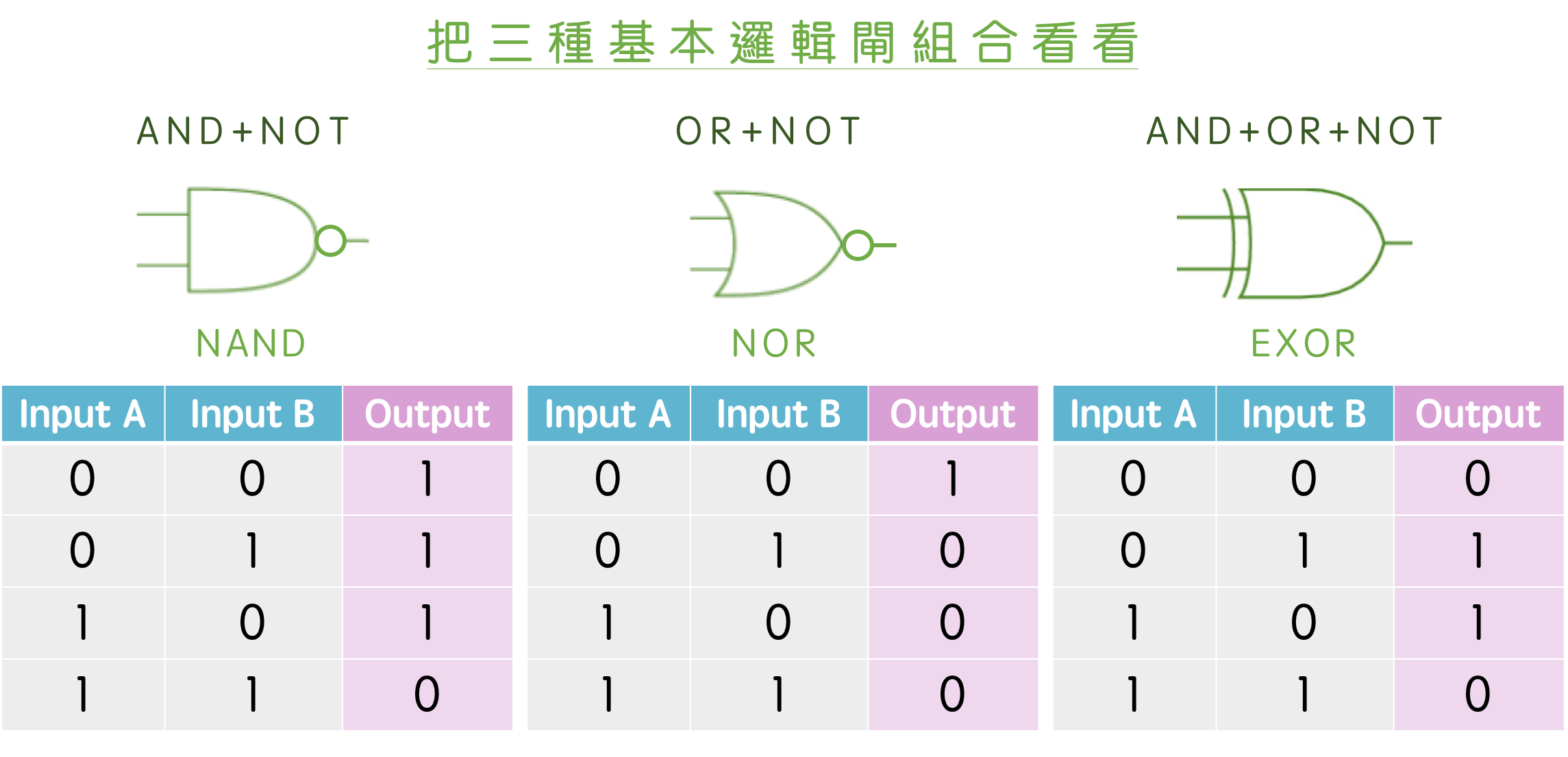
另外,只要利用 AND、OR、NOT 三款基本電路,就可以拼出所有其他種組合的電路:
- 「NAND」 = AND + NOT:反轉 AND 的結果。兩個都不同意、或一個不同意時都是 yes;但兩個都同意反而變成 no。
- 「NOR」 = OR + NOT:反轉 OR 的結果。
- 「EXOR」 = AND + OR + NOT:如果爸媽的意見相同 (都是 0 或都是 1 ) 就輸出 0、如果意見不同則輸出 1。
(3) 如何用電路實現?
知道數字該如何表示與運算的方法後,要怎麼實作出一個真正有功能的電路呢?(知道 AND、OR、NOT 沒用啊,重點是要真的能運算數字!)
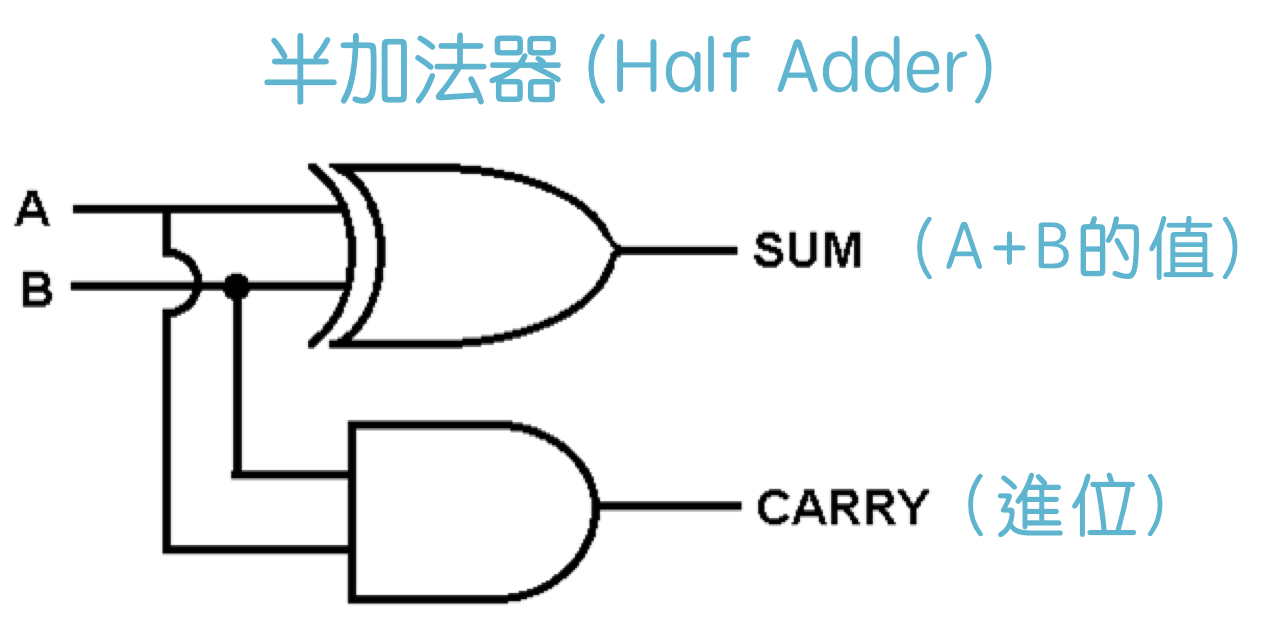
也就是說,把 EXOR 電路和 AND 電路組合在一起,便能進行一位元(一個位數)的加法!一位數加法的意思是 0+0, 0+1, 1+0, 1+1。
所以這就是具備兩個輸入(A、B)和兩個輸出(Sum加總 和 Carry進位)的半加法器!
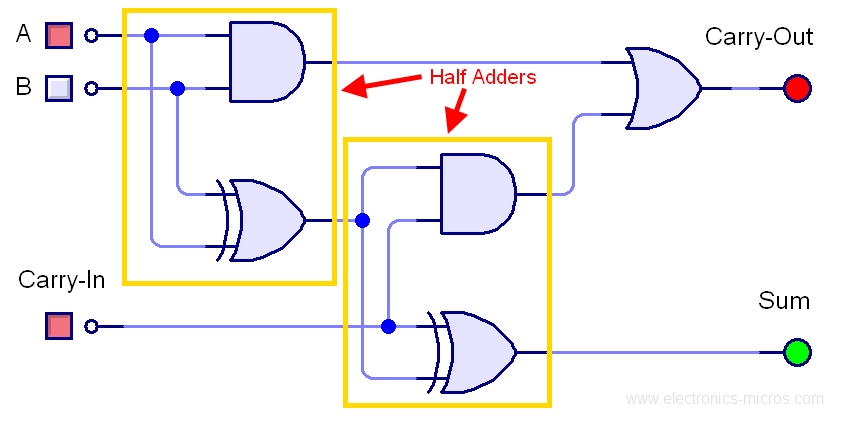
但半加法器只能進行一個位數的加法,該怎麼辦呢…?只要使用兩個半加法器,便能做出全加法器噢!
全加法器能做「兩個位數」的加法。它具備了三個輸入(A, B, Carry-In)與兩個輸出(A+B, Carry-Out)。Carry-In 代表進位的輸入、Carry-Out 代表進位的輸出。
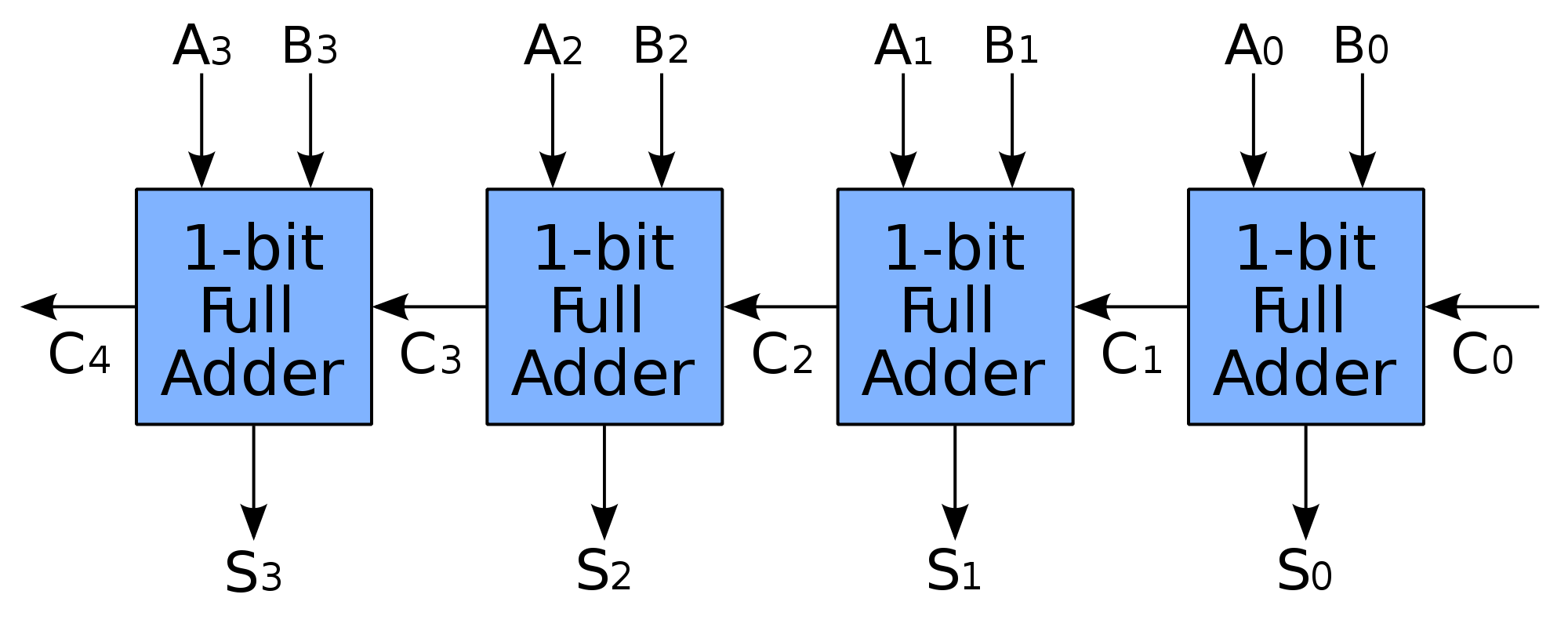
很顯然,只要不斷增加全加法器,就能做出多個位數的加法電路。這就叫做「漣波進位加法器」(Ripple Carry Adder)。像下圖中有四個加法器,能進行四位數的加法!
把加法器造出來後,電路的運算也就成功完成了!
等等,四則運算不是還有減法和乘法、除法嗎?你只講了加法耶…
還記得我們上面提到的補數嗎?減法可以藉由一個數加上補數的加法解決。(比如說「1 – 2」可以看成「1 + (-2)」,也就是「001 ( 1 的二進數) + 110 ( 2 的二進位補數)」)
乘法就是連續的加法、除法就是連續的減法。所以有了一個加法器,等同於能造出所有基本運算了!
(當然加法器有好幾種、漣波進位加法器只是最簡單的其中一種而已;乘法器和除法器也是… 不過總之有個概念就好,其他讀者有興趣的話再自己去研究吧)
噢~~~我們終於成功解決一開始問的三個問題了!
(1) 數字在計算機中該如何表示?
(依據目前的計算與儲存技術)二進位制。遇到負數就使用 2’s 補數法。
如果某天採用 DNA 儲存技術,或不用馮紐曼、改用量子電腦架構,就不一定是用二進位制了。
(2) 數字在計算機中如何運算?
布林代數的邏輯運算。
(3) 如何用電路實現?
用 AND+EXOR 基本電路做出半加法器後,再把半加法器合成全加法器,再把全加法器組合起來、就能進行多位數的運算。
如果想要運算減法,就用加補數的方式;想運算乘法就使用連加、運算除法就用連減。
看起來似乎都結束了,但感覺還是有哪邊怪怪的…?(大家看文章時要積極思考提問啊~~)
奇怪,電路圖怎麼不是一堆電線,而是這種奇怪的符號呢?總不會我打開這顆 IC 的封裝後,真的會看到這些 AND、OR、NOT 三角形橢圓形的邏輯閘吧… (´A`。)?為什麼電路圖的畫法不是一堆電路線?
當然不會看到這些符號。邏輯電路圖只是用來描述電路行為的抽象電路圖。
什麼是電路行為、抽象???(暈倒)…( ×ω× )
另外,還記得我們一天到晚聽到:「摩爾定律下、晶片上的電晶體數量每兩年就增加一倍,現在的晶片中有數億個電晶體…」但我們從沒聽懂過,這個電晶體到底是做什麼用的呢?
其實電晶體的功用,就是用來當邏輯閘。
… 但上面看起來一點都不像電晶體啊(難道電晶體長的是像橢圓形或三角形)?為什麼電路圖不直接畫出電晶體呢?
咳咳,就讓我們在下集為大家繼續解釋吧。