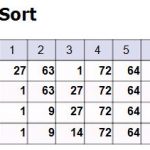
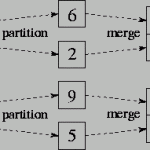
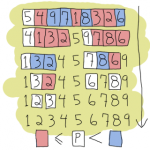
之前介紹過的插入排序、選擇排序、泡泡排序等方法雖然簡單,在演算法的執行效率上卻犧牲了很多,時間複雜度高達 O(n2 )。
現在要介紹的快速排序 (Quick Sort) 是平均狀況下,排序時間最快的方法。
Quick Sort 採用 Divide-and-Conquer 策略──也就是將一個問題切割成幾個獨立的子問題,最後合併所有子問題上的最佳解,作為整個問題的最佳解。
歡迎參考 edX 上開授的 CS 50 課程示範影片:
https://www.youtube.com/watch?v=aQiWF4E8flQ
在數列中隨便找一個數字作為基準 (pivot),然後把該數列中所有比基準數小的數字都放在左邊、比基準數大的數字都放在右邊。
即代表此陣列已經被切割成左、右兩個子陣列。再讓左右兩個子陣列各自做排序,當左、右子陣列排完時,整個排序也就結束了。
關鍵問題是,如何做 Partition (分割)?這個問題也就是如何決定基準的正確位置。
虛擬碼 (這裡的虛擬碼是cormen演算法書上提供的作法)
Partition(A, left, right)
pivot = A[right]
i = left-1
for j = left to (right-1) do
if (pivot>=A[j])
i = i+1
swap(A[i], A[j])
end if
end for
swap(A[right], A[i+1])
return (i+1) //回傳pivot的正確位置
QuickSort(A, left, right) //排序A[left]~A[right]
if(left<right) then
i = Partition(A, left, right)
QuickSort(A, left, i-1)
QuickSort(A, i+1, right)
end if
用最後一格當作 pivot。
程式碼(這裡是hORWITZ提供的作法)
#include <stdio.h>
void swap(int *a, int *b){
int temp;
temp = *a;
*a = *b;
*b= temp;
};
int quick_sort(int A[], int left, int right) //排序A[left]~A[riht]
{
int pivot;
int i, j;
if(left < right){
pivot = A[left];
i = left;
j = right+1;
while(i<j){
while(pivot>A[i])
i++;
while(pivot<A[j])
j--;
if(i<j) //直到i ,j兩軍交會
swap(&A[i], &A[j]);
}
while(i<j) //要不要加這個while??
swap(&A[left], &A[j]);
quick_sort(A, left, j-1);
quick_sort(A, j+1, right);
}
};
int main(){
int count, i;
scanf("%d", &count);
int list[count];
printf("Numbers to be sorted: ");
for(i = 0; i<count; i++){
scanf("%d", &list[i]);
printf("%d ", list[i]);
}
printf("\n");
quick_sort(list, 0, count-1);
printf("Numbers Sorted: ");
for(i = 0; i<count; i++){
printf("%d ", list[i]);
}
printf("\n);
return 0;
}
時間複雜度
1. Best Case: O(n log n)
Pivot 的正確位置恰好將資料陣列切割成兩等分。
- c*n: Partition 所花時間為 O(n) 或 c*n
- T(n/2) 分別為左、右串列遞迴做 Quick Sort 的時間
,其中 c 為正常數, T(1) = 0
故時間複雜度為 O(n log n)
2. Worst Case: O(n2)
Pivot 恰好是該資料陣列的最小值或最大值,使得切割無法產生一分為二的效果。
T(n) = c*n + T(n-1) + T(0), c*n 為切割時間
T(n) = T(n-1) + c*((n-1)+n) = … = T(1) + c*(2+ … +n)
故時間複雜度為 O(n2)
避免 Quick Sort 的 Worst Case 發生
有鑑於時間複雜度高達 n2,要怎麼樣才能避免取到最小或最大值的 Worst Case 呢?
以下提供三種可能解法:
1. Middle-of-Three 方法
(1) 令 middle = (left + right) /2
(2) 比較 A[left]、A[middle] 與 A[right] 這三筆資料,排出中間值。
c. 將此中間值再與 A[left] 做交換
(3) 讓現在新的 A[left] 作為 pivot
如果 pivot 的位置恰好在 n 筆資料中的 n/10 與 9n/10 之間:
c*n ----------c*n
/ \
c*n/10 c*9n/10-----c*n
/ \ / \
... ... ... ... ---c*n
T(n) = c*n + T(n/10) + T(9n/10)
還是可以收斂到 O( n log n)。
2. Randomized Quick Sort
用亂數選取的方式,隨機挑一個值作為 pivot。
當然,這還是可能會發生 Worst Case 高達 O(n2) 的問題,只是機率比較低。Average Case 與 Best Case 同樣是 O(n log n)。
所以我們也可以把以上兩種改進合併──先用亂數任選三個,再用其中的中間值作為 pivot。
3. 使用 Median-of-Medians 作為基準
(1) 將 n 個資料分成 n/5 個堆,每堆有 5 個資料 (可能會有 1 個堆的資料不到 5 個) ,共花 O(n) 時間。
(2) 每堆各由小到大做排序。排序一堆得花 O(52) 時間,可以想成 O(1) 常數。所以當有 n/5 堆排序時,共花 O(n) 時間。
(3) 將排序完、將每堆的第 3 個資料 (也就是中位數) 作為該堆的中間鍵。在這 n/5 堆中,遞迴套用此演算法,求得求出中位數們的中位數 k。 k 即為 median-of-medians ,此步驟花費時間 T(n/5)。
(4) 以 k 作為 pivot 重新將堆做排序,花 O(n) 時間。
到這個步驟為止,所花費的時間:T(n) = O(n) + O(n) +T(n/5) + O(n) + ???。問號的地方就是來看看第 (5) 個步驟:
(5) 至少有一半的堆(扣掉 pivot 自己、及不到 5 個資料的堆)、每堆必有 3 個資料大於等於 pivot。
也就是說,至少會有 個資料,化簡為
個資料大於等於 pivot。
(7n/10)+6 個資料---------pivot ---- (3n/10)-6 個資料
此 (5) 步驟的 Worst Case 為 。
全部步驟的 Worst Case 即為
c*n -----------c*n
/ \
c*n/5 c*7/10n------c*9/10*n
/ \ / \
... ... ... ... ----c*(9/10)^2*n
可知最後的時間複雜度成功降到了 O(n)!
空間複雜度
位於 O(log n) ~ O(n) 之間。額外空間需求來自於遞迴所需的 Stack 空間,而 Stack Size 取決於 Recursive Call 的次數。
1. Best Case:
經過 k 次的遞迴呼叫後,達到 1 筆資料後即可停止。
n/2 筆資料 --------- pivot --------- n/2 筆資料 n/4 筆資料 --- pivot --- n/2 筆資料 n/8 筆資料 -- pivot -- n/8 筆資料 ... 1 筆
$latex \frac{n}{2^{k}} $ = 1 筆,故 $latex k = \log_{2}n $ 。
2. Worst Case:
pivot 為最大或最小值
pivot ------------ (n-1) 筆資料
pivot ------- (n-2) 筆資料
pivot -- (n-3) 筆資料
...
(n-k) = 1 筆資料
k = n-1,故空間高達 O(n)。
穩定性: UNSTABLE
input data: 3 , 5 , 5* , 1 , 2 pivot: 3 -------------------------------- Pass 1: 3 , 2 , 5* , 1 , 2 Pass 2: 3 , 2 , 1 , 5*, 5 Pass 3: 1 , 2 , 3 , 5* , 5
可以發現到最後 5 和 5* 的位置交換了。