本篇將為大家介紹插入排序 (Insertion Sort) 的原理、虛擬碼、程式碼與時間複雜度分析。
插入排序
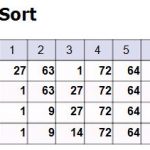
概念有點類似平常玩的撲克牌。當莊家發牌時,玩家拿到第一張牌、接著拿到第二張牌的時候,就會先把兩張作比較排序好。
接下來第三張牌接著插入這堆已經排序好的排組,接著同理。直到撲克牌發完的時候,手上的撲克牌也已經依照點數大小排序好了。
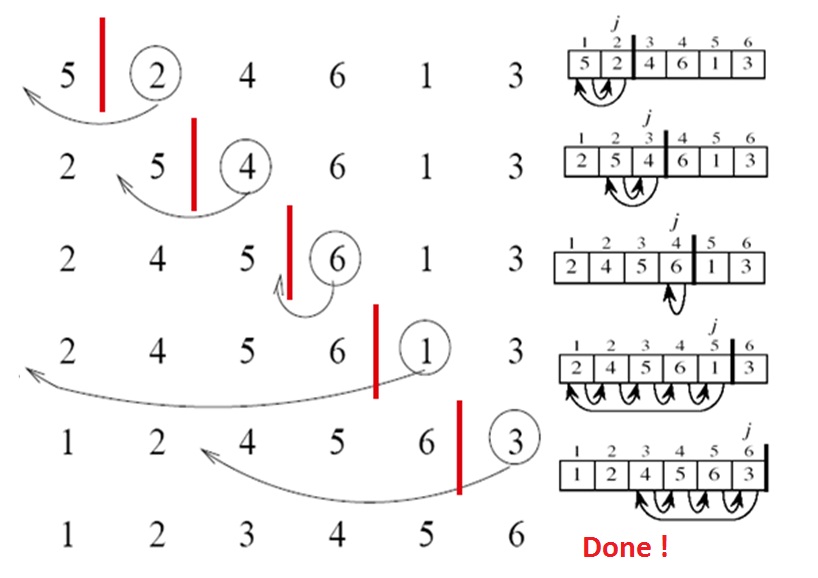
虛擬碼
for j = 2 to A.length do //A為此堆資料的陣列
data = A[j] //data為要插入的資料
i = j-1
while i > 0 and A[i] > data do
A[i+1] = A[i]; //若新插入的資料比較小,就把已經排序好的原資料向後移
i = i-1; //繼續向前檢查,直到新插入資料比較大為止
end while
A[j+1] = data; //最後將空下來的位置讓給新插入的資料
end for
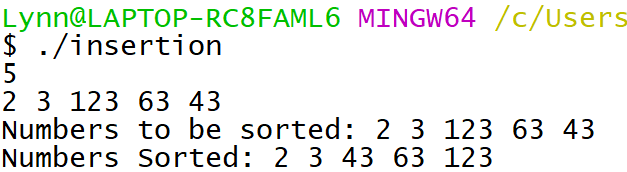
程式碼
i = 2 開始,做 n-1 個回合──將第 i 筆資料插入前面 i-1 筆已排序好的資料,形成 n 筆排序好的資料。
原先想法:
- insert(list[], data, n) 作為副程式
- insort(list[], n) 作為主程式
#include <stdio.h>
int insert(int poker[], int card, int n) //把card插入前第0~n筆已排序好的資料
{
int j = n;
while(card < poker[j])
{
poker[j+1] = poker[j];
j--;
}
poker[j+1] = card;
return 0;
}
int insort(int poker[], int count) //排序第poker[1]到poker[count]筆資料
{
int i;
for(i = 2; i<=count; i++)
{
insert(poker, poker[i], i-1);
}
printf("Numbers Sorted: ");
for(i = 1; i<=count; i++)
{
printf("%d ", poker[i]);
}
printf("\n");
return 0;
}
int main()
{
int count;
scanf("%d", &count);
int poker[count];
poker[0] = -1000000;
int i;
printf("Numbers to be sorted: "); //印出待排序數字
for(i = 1; i<=count; i++)
{
scanf("%d", &poker[i]);
printf("%d ", poker[i]);
}
printf("\n");
insort(poker, count);
return 0;
}
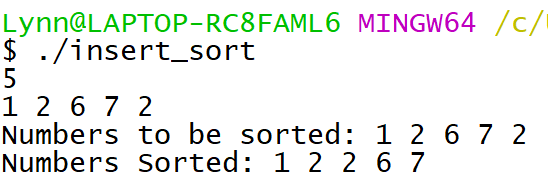
其他的寫法:這個實現方式比較接近虛擬碼
從第二個資料開始,如果第二個資料比第一個資料大,順序就維持不變;否則將第一個資料往後移動,然後將第一個資料空下來的位置讓給第二個資料。
此時第一和第二個資料就由小到大排序完成。
同理,依序移動資料直到第 n 筆資料都排序完成。
#include <stdio.h>
int insertion_sort(int poker[], int n){
int i, j, card;
for(i = 1; i < n; i++){ //從第二張牌開始跟前面的撲克牌比大小
card = poker[i];
for(j = i-1; j>=0 && card<poker[j]; j--){ //把card插入前面排序好的撲克牌
poker[j+1] = poker[j];
}
poker[j+1] = card;
}
};
int main(){
int count, i;
scanf("%d", &count);
int poker[count];
for(i = 0; i < count; i++){
scanf("%d", &poker[i]);
}
printf("Numbers to be sorted: ");
for(i = 0; i<count; i++){
printf("%d ", poker[i]);
}
insertion_sort(poker, count);
printf("\n");
printf("Numbers Sorted: ");
for(i = 0; i<count; i++){
printf("%d ", poker[i]);
}
return 0;
}
時間複雜度
1. Best Case: O(n)
若 input data 剛好是由小到大的方式給予,每一回合只需比較一次,即可決定好要插入 data 的正確位置。
又共做了 n-1 回合,故總共比較 n-1 次即可完成 sort。
如果利用 Recursive Time Function 來解時間複雜度,同樣會得到 O(n) 的結果:
T(n) = T(n-1)+1, T(1) = 0
----------------------------------
T(n) = T(n-1)+1
= T(n-2)+2
= ...
= T(1)+(n-1) //帶入T(1) = 0
= n-1
=> O(n)
2. Worst Case: O(n2)
若 input data 剛好是反序由小到大給予。
input: n, n-1, n-2, ... , 2, 1 比較次數
------------------------------------------------------
Pass 1: (n-1), (n), n-2, ... 1 次
Pass 2: (n-2), (n-1), (n), n-3, ... 2 次
Pass 3: (n-3), (n-2), (n-1), (n), n-4, ... 3 次
...
Pass (n-1): (n-1) 次
Total = 1 + 2 + 3 + ... + (n-1)
= n(n-1)/2 次比較
=>O(n^2)
如果利用 Recursive Time Function 來解時間複雜度,同樣會得到 O(n2) 的結果:
T(n) = T(n-1)+(n-1), T(1) = 0
//n-1代表第n筆data插入之最多比較次數
----------------------------------
T(n) = T(n-1)+(n-1)
= T(n-2)+(n-2)+(n-1)
= ...
= T(1)+1+...+(n-1) //帶入T(1) = 0
= 1+2+...+(n-1)
= n(n-1)/2
=> O(n^2)
3. Average Case: O(n2)
T(n) = T(n-1)+(n/2), T(1) = 0
//n/2代表第n筆data插入之平均比較次數
----------------------------------
T(n) = T(n-1)+(n/2)
= T(n-2)+1/2[(n-1)+n]
= ...
= T(1)+1/2[2+...+n] //帶入T(1) = 0
= 1/2*{(n+2)(n-1)/2}
=> O(n^2)