搜尋與排序 (Search & Sort)

排序是相當常見的電腦運算，目的通常有兩個：

1. 搜尋 (searching)

2. 比對 (matching)

也就是說，要先做完排序後，才好做後面的搜尋。

排序演算法有很多，知名的包括：

• 選擇排序 (Selection Sort)
• 插入排序 (Insertion Sort)
• 泡泡排序 (Bubble Sort)
• 快速排序 (Quick Sort)
• 希爾排序 (Shell Sort)
• 合併排序 (Merge Sort)
• 基數排序 (Radix Sort)
• 二元樹排序 (Binary Tree Sort)
• 堆積排序 (Heap Sort)

我們可以根據幾種規則，將排序方式加以分類：

> 資料存放位置：Internal Sorting / External Sorting

外部排序 (External Sorting)──資料量太大，無法一次全部置於記憶體中進行排序，必須藉由外部儲存體 (比如硬碟) 保存資料再進行排序。否則為內部排序 (Internal Sorting)。

常用的外部排序方式有 Merge Sort、m-way Search Tree、B Tree。

> 排序後，鍵值相同的資料相對位置是否改變：Stable/ Unstable

通常待排序的資料可能會出現重複的資料值，比如 {7, 2, 3, 3*, 4, 9} 其中 3* 代表第二個 3。如果經過排序後，結果保證 3 還是會在 3* 前面，稱為穩定排序 (Stable Sorting)，否則為不穩定排序 (Unstable Sorting)。

> 排序效率：初等排序 / 高等排序

若排序方法較簡單、執行時間較長、時間複雜度為 O(n²)，稱為初等排序，包括：選擇排序、插入排序、泡泡排序。

若排序方法較複雜、執行時間較短、時間複雜度為 O(n log2 n)，稱為高等排序，包括：快速排序、合併排序、基數排序… 等。

 

Linear Search (線性搜尋)

定義

又叫作 Sequential Search，即從頭到尾一一比較各點 data 值，直到找到、或搜尋完整個範圍仍找不到為止。

特點

(1) 資料搜尋之前無需事先排序

(2) 資料存於 sequential access (比如鏈結串列) 或 random access (比如陣列) 機制皆可支持。

時間複雜度

平均比較次數 = $latex \frac{\left ( 1+2+3+ \cdots + n \right )}{n} = \frac{\left ( n+1 \right )n}{2}*\frac{1}{n} =\frac{n+1}{2} $

資料量少時，使用 linear search 即可；資料量大時使用 Binary Search。

虛擬碼

LinearSearc(A[], key){
  for i = 1 to n do
  {
    if (A[i] == key)
      return i;
    else
      return NIL;
  }
}

 

程式碼

#include <stdio.h>

int linear_search(int A[], int n, int key){
  int i;
  int flag = 0;
  for(i = 0; i<n; i++){
    if(key == A[i]){
      flag = 1;
      printf("Found! Position: %d\n", i+1);
    }
  }
    if(flag == 0){
      printf("Not Found!\n");
    }
}

int main(){
  int n, i, key;
  printf("Enter array length: ");
  scanf("%d", &n);
  int list[n];
  printf("Enter sorted numbers: ");
  for(i = 0; i<n; i++){
    scanf("%d", &list[i]);
  }
  printf("Current numbers: ");
  for(i = 0; i<n; i++){
    printf("%d ", list[i]);
  }
  printf("\n");
  printf("Enter key: ");
  scanf("%d", &key);
  linear_search(list, n, key);
  return 0;
}

Binary Search (二分搜尋)

只要將欲搜尋的資料值和位於陣列中間的資料做比較，若欲搜尋的值比較大，表示該值可能位於陣列的中間到後面；否則是位於陣列的前面到中間。

此時可以將搜尋的範圍縮小一半，再用相同的方式在可能範圍內進行搜尋，直到找到值符合的資料，把其 Array Index 回傳回來。

顯然 Binary Search 平均比較次數比 Linear Search 還少。

實施前提

1. 資料必須事先由小到大排序好

2. 資料是用 random access 機制 (例如 Array) 存放才可支援。

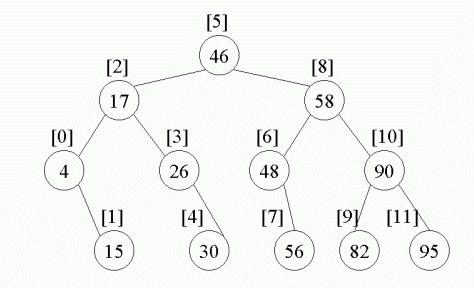
利用 Decision Tree，可以把 Binary Search 搜尋過程演示出來。

Array Index|[0]  [1]  [2]  [3]  [4]  [5] [6] [7]  [8]  [9]  [10] [11]
Input Data | 4 , 15 , 17 , 26 , 30 , 46, 48 , 56 , 58 , 82 , 90 , 95

虛擬碼 (ITERATIVE 版本)

BinSearch(A[], min, max, key) 
//在 A[min]~A[max]已由小到大排序好的資料中，尋找有無key存放
  left = min
  right = max
  while (left<=right)
    mid = (left+right)/2
    if key == A[mid]
      return mid
    else if key < A[mid]
      right = mid-1
    else //key>A[mid]
      left = mid+1
  end while

 

程式碼

#include <stdio.h>

void binary_search(int A[], int key, int n){
  int left, right, mid;
  left = 0;
  right = n-1;
  while(left<=right){
    mid = (left+right)/2;
    if(key == A[mid]){
      printf("Found! Position: %d", mid+1);
      printf("\n");
      break;
    }
    else if(key<A[mid]){
      right = mid-1;
    }
    else if(key>A[mid]){
      left = mid+1;
    }
    else{
      printf("Not Found!");
      printf("\n");
      break;
    }
  }
}

int main(){
  int n, i, key;
  printf("Enter array length: ");
  scanf("%d", &n);
  int list[n];
  printf("Enter sorted numbers: ");
  for(i = 0; i<n; i++){
    scanf("%d", &list[i]);
  }
  printf("Current numbers: ");
  for(i = 0; i<n; i++){
    printf("%d ", list[i]);
  }
  printf("\n");
  printf("Enter key: ");
  scanf("%d", &key);
  binary_search(list, key, n);
  return 0;
}

虛擬碼 (RECURSIVE 版本)

BinSearch(A[], min, max, key)
  if min<max then
    mid = (min+max)/2
    if(key==A[mid])
      return mid //找到資料
    else if(key<A[min])
      return BinSearch(A, min, mid-1, key)
    else
      return BinSearch(A, mid+1, max, key)
  end if

 

程式碼

#include <stdio.h>

int binary_search(int A[], int left, int right, int key){
  int mid;
  if(left<=right)
  {
    mid = (left+right)/2;
    if(key == A[mid]){
      printf("Found! Position: %d", mid+1);
      printf("\n");
    }
    else if(key<A[mid]){
      binary_search(A, left, mid-1, key);
    }
    else if(key>A[mid]){
      binary_search(A, mid+1, right, key);
    }
    else{
      printf("Not Found!");
      printf("\n");
    }
  }
}

int main(){
  int n, i, key;
  printf("Enter array length: ");
  scanf("%d", &n);
  int list[n];
  printf("Enter sorted numbers: ");
  for(i = 0; i<n; i++){
    scanf("%d", &list[i]);
  }
  printf("Current numbers: ");
  for(i = 0; i<n; i++){
    printf("%d ", list[i]);
  }
  printf("\n");
  printf("Enter key: ");
  scanf("%d", &key);
  binary_search(list, 0, n-1, key);
  return 0;
}

時間複雜度

令 T(n) 代表使用 Binary Search在 n 筆資料中找 key 所花的時間。

T(n) = 1 + T(n/2), T(1) = 1

T(n) = 1 + 1 + T(n/4) = … = T(1) + log n = 1 + log n

故時間複雜度為 O(log n) 。

 

接著，讓我們來試著跑跑看 1000 筆資料，比較一下 O(n) 時間的 Linear Search 與 O(logn) 時間的 Binary Search 效率的差異吧！

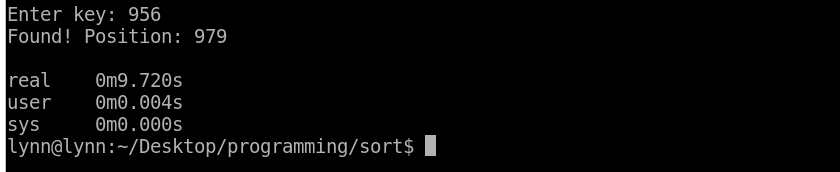
Linux 有個有趣的指令「time」，可用來查看一程式或指令的執行時間──只要在 Terminal 中輸入「 time ./檔名.exe」，即能顯示這支程式的執行時間。

time 指令的返回值包含「實際時間 (real time)」、「用戶 CPU 時間 (user CPU time)」及「系統 CPU 時間 (system CPU time)」。

• real time 代表該指令或程式從開始執行到結束終止所需要的時間。
• user CPU time 表示程式在 user mode 所佔用的 CPU 時間總和。多核心的 CPU 或多顆 CPU 計算時，則必須將每一個核心或每一顆 CPU 的時間加總起來。
• system CPU time 表示程式在 kernel mode 所佔用的 CPU 時間總和。

在這邊我們只要看 real time 的時間就好。

輸入 1000 筆已經排序好的資料 (由小到大)，輸入希望尋找的數字「956」，無論是 Linear Search 還是 Binary Search，運行結果都是找到位置於「979」。

來看看 Linear Search 跑出來的時間：2 分 42 秒…

Binary Search 的 Iterative 版本：26 秒

Binary Search 的 Recursive 版本：9 秒

資料量雖然相同，卻是不是差距很大呢！