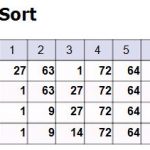
「二元樹」是電腦科學最重要的概念,甚至可以說:二元樹開創了電腦科學。
像是資料結構 Binary Search Tree 與 Heap ,交換式排序演算法的 Decision Tree 、資料壓縮的 Huffman Tree 、 3D 繪圖的 BSP Tree 、編譯器的 Parse Tree…… 這一大堆稀奇古怪的術語,通通都是二元樹。(節錄自 演算法筆記)
樹 (Tree)
1. 定義
- 由 1 個以上的節點所構成的集合,不可為空。
- 至少有一個特殊節點,稱為 Root。
- 其餘 Nodes 分成
個互斥集合,稱為 Root 的子樹 (subtree)。
2. 術語
1. Node’s Degree (分支度)
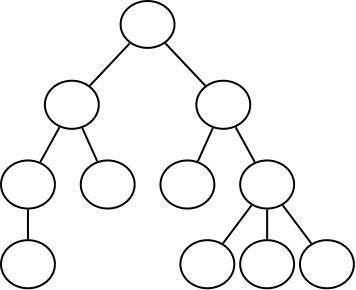
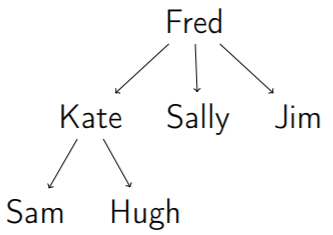
e.g. Fred 節點的分支度為 3、Kate 節點的分支度為 2。
2. Tree’s Degree = Max{各節點的分支度}
e.g. 此棵樹的分支度為 3 。
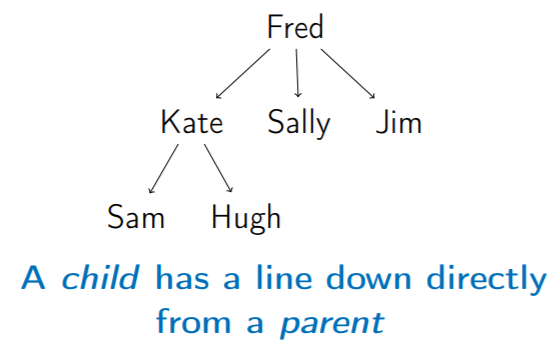
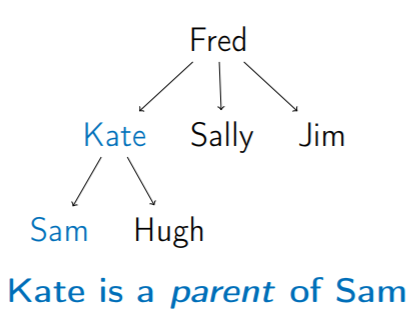
3. Child (子點) & Parent (父點)
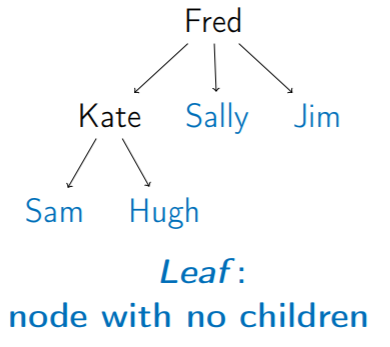
4. Leaf (樹葉):Degree = 0 的節點 (沒有 child )
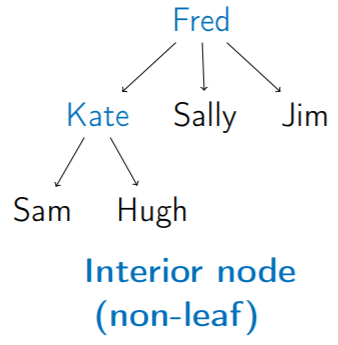
5. Non-Leaf (內部節點)
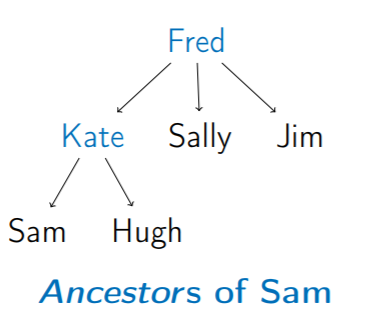
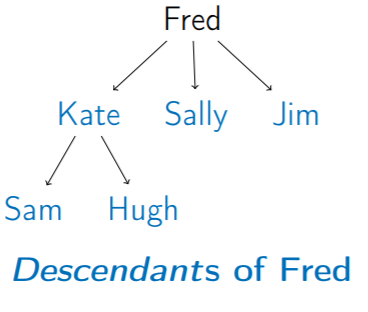
6. Ancestors (祖先) & Descendants (後代)
7. Node’s Level (階層)
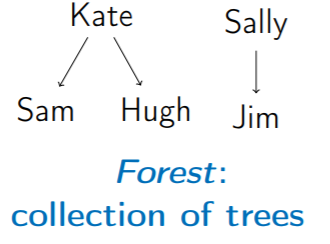
e.g. Fred 的階層為 1、Kate&Sally&Jim 的階層為 2、Sam&Hugh 的階層為 3。
8. Tree’s Height = Max{各節點的階層}
此棵樹的高度為 3。
9. Forest (森林):由 >=0 棵互斥 Trees 所形成的集合,可以為空。
3. 表示方法
1. 括號法
以 父點(子點1, …, 子點m) 表示父子組成關係。
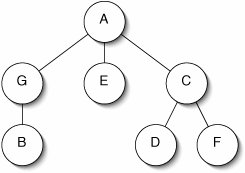
e.g. 可將此樹表示為 A(G(B)EC(DF))
2. 利用 Linked List
假設這棵樹有 n 個節點,分支度為 k ,則 Node Structure:
缺點:極度浪費鏈結欄位的空間。
節點個數取決於樹的分支度,一個節點數為 n、分支度 k 的樹將有 n*k 個鏈結欄位。其中有使用到的鏈結欄位只有 n-1 條 (即等於邊數)。
這表示空鏈結欄位數為 n*k-(n-1),浪費比例為
為了節省記憶體,令 k-1 = 1、 ,也就是把樹化為二元樹 (Binary Tree) 再予以表示。
二元樹
1. 定義
每個節點最多只有兩個子節點的樹,節點左邊稱為左子樹 (left child)、節點右邊稱為右子樹 (right child)。
- 可以為空集合。(比較: 樹不可為空集合, 須至少有 1 個 Root)
- 節點分支度 <= 2。(比較: 樹 Non-Leaf 節點的分支度須 > 0)
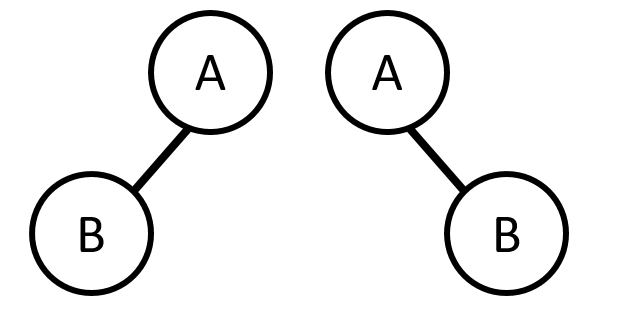
- 子樹有左、右方向的分別。(比較: 樹的子樹無方向之分)
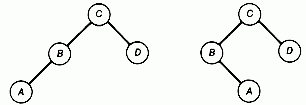
e.g. 此為兩棵相同的樹,但是是兩棵不同的二元樹。
證明:二元樹第 i Level最多節點個數為 2^i-1
利用數學歸納法:
1. 當 level = 1 時,最多只有 Root 一個節點,符合 $latex 2^{i} -1 = 2^{0} = 1 $ ,故成立。
2. 令 level = (i-1),此定理成立,也就是第 (i-1) level 最多節點數為 $latex 2^{i-2}$ 。
3. 當 level = i 時,最多節點數必定是第 (i-1) level 的最多節點數 *2。
Q.E.D.
證明:高度 K 之二元樹,最多節點數為 2^K-1,最少節點數為 k
由於二元樹第 i 階的最多節點個數為 $latex 2^{i-1} $ ,每一層之最多節點數加總:。
也就是說,若二元樹有 n 個節點:
- 最大高度為 n
- 最小高度為 $latex 2^{k} -1 = n $,$latex 2^{k} = n+1 $,
2. 種類
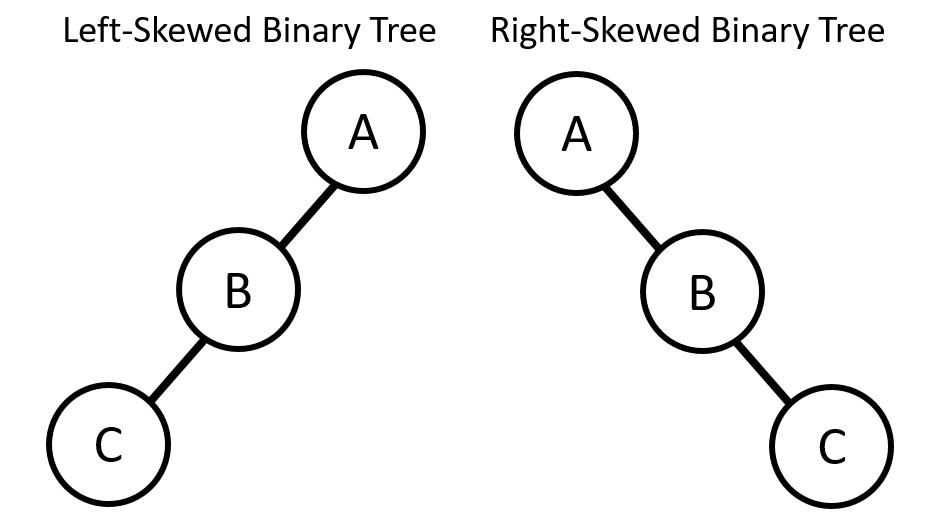
1. skewed tree (斜區樹)
- Left-Skewed Binary Tree:每個 Non-Leaf 皆只有左子點
- Right-Skewed Binary Tree :每個 Non-Leaf 皆只有右子點
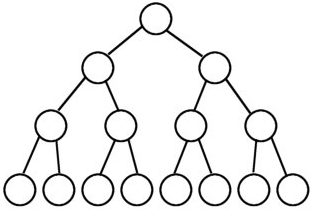
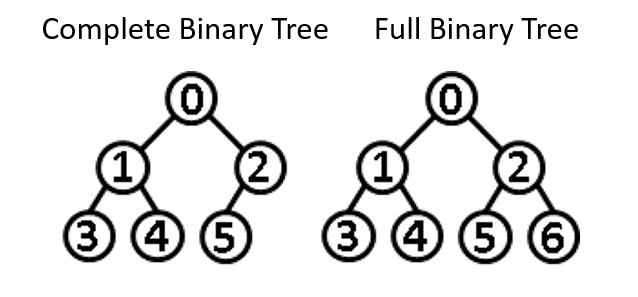
2. 完滿二元樹 (full binary tree)
高度 k 且節點個數 $latex 2^{k} -1 $ 、具有最多節點的二元樹。除了 Leaf 以外,每個節點都有兩個 child。
3. 完整二元樹 (complete binary tree)
高度 k、節點個數 n 且滿足:
。也就是各層節點全滿,除了最後一層,最後一層節點全部靠左。
- 節點順序晦暗高度為 k 的完滿二元樹的前 n 個節點編號一一對應。
3. 實作
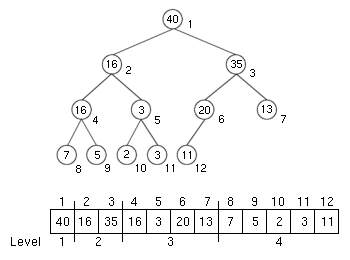
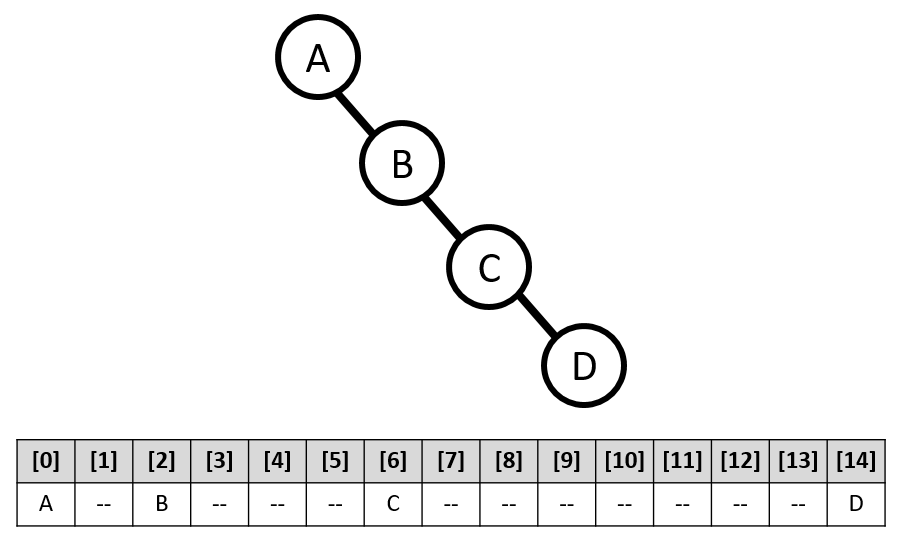
1. 使用陣列
優點是容易實作,且能快速找到任意節點的父節點與左右子節點。
- 陣列 index 為 i
- parent 位置: (i-1)/2
- left-child 位置: 2*i+1
- right-child 位置: 2*i+2
缺點是當二元樹稀疏或不平衡時,就會相當浪費記憶體。故較為適用於 Complete Binary Tree 或 Full Binary Tree,較不適用於 Skewed Binary Tree。
另一個缺點是增加和刪除節點時,需要搬移多個節點。
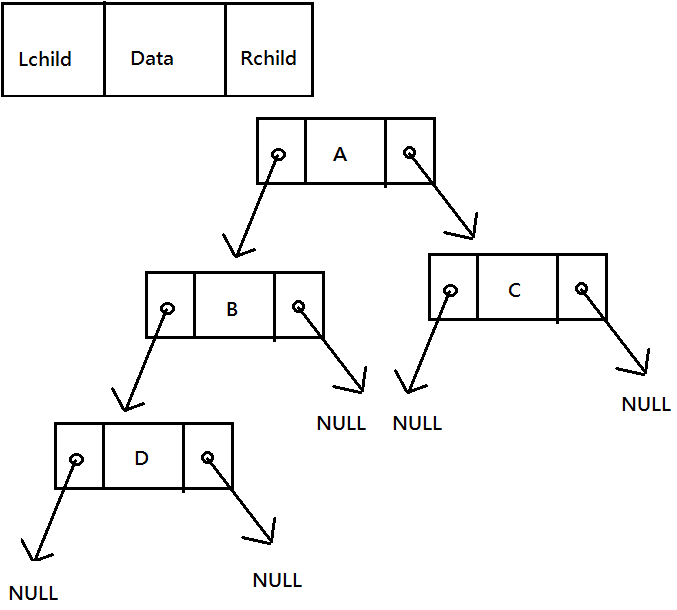
2. 使用鏈結串列
Lchild 欄位用來存放指向左子點的左鏈結,Rchild 欄位用來存放指向右子點的右鏈結。data 欄位用來存放節點資料。
struct Node{
Node* Lchild;
Node* Rchild;
int data;
};
3. 走訪 (Traversal)
拜訪每個節點各一次。則二元樹的走訪可以有 3! = 6 種走訪組合 (D: Root, L: 左子樹, R: 右子樹):
- DLR
- DRL
- LDR
- LRD
- RDL
- RLD
由於我們必須限制先走左子樹、再走右子樹,因此 L 必在 R 之前走訪。只剩下三種結果:
- DLR: 前序 (Preorder)
- LDR: 中序 (Inorder)
- LRD: 後序 (Postorder)
若再加上一種走訪:Level-Order Traversal,乃依照 Level 由上而下,同一 Level 由左而右依序拜訪節點。
NOTE: 前中後序使用STACK實作(遞迴),LEVEL-ORDER 使用QUEUE實作
1. 前序
preorder(Node *root){
if(root == NULL) return;
printf("%d", root->data);
preorder(root->Lchild);
preorder(root-<Rchild);
}
2. 中序
inorder(Node *root){
if(root == NULL) return;
inorder(root->Lchild);
printf("%d", root->data);
inorder(root-<Rchild);
}
3. 後序
postorder(Node *root){
if(root == NULL) return;
postorder(root->Lchild);
postorder(root-<Rchild);
printf("%d", root->data);
}
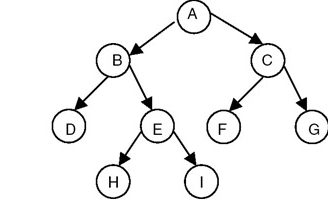
以前序為例,實際演練看看這個遞迴程式:
印出 A
走訪 A 左子樹
印出 B
走訪 B 左子樹
印出 D
走訪 D 左子樹,空子樹
走訪 D 右子樹,空子樹
走訪 B 右子樹
印出 E
走訪 E 左子樹
印出 H
走訪 H 左子樹,空子樹
走訪 H 右子樹,空子樹
走訪 E 右子樹
印出 I
走訪 I 左子樹,空子樹
走訪 I 右子樹,空子樹
走訪 A 右子樹
印出 C
走訪 C 左子樹
印出 F
走訪 F 左子樹,空子樹
走訪 F 右子樹,空子樹
走訪 右 左子樹
印出 G
走訪 G 左子樹,空子樹
走訪 G 右子樹,空子樹
根據走訪過程,此前序走訪結果為:ABDEHICFG
同理,此棵樹的中序走訪結果為:DBFEIAFCG;後序走訪結果為:DHIEBFGCA。
給予二元樹的「前序, 中序」或「後序, 中序」,可決定唯一一個二元樹。但「前序, 後序」可能會得到大於 1 棵的二元樹。
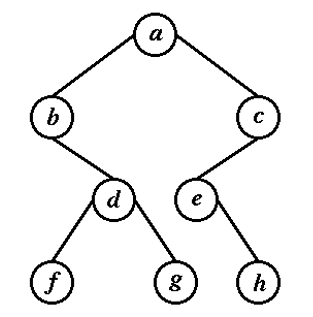
例. 前序: abdfgceh, 中序: bfdgaehc, 決定此 B.T.
- 前序: 第一點為 Root,即 a
- 中序: 切出左子樹與右子樹之集合
例. 前序 CBAD, 後序 ABDC 無法決定唯一的 B.T.