介紹遞迴的原理,與經典題型:最大公因數 (GCD)、費波納契數列 (Fibonacci Sequence)、河內塔 (Hanoi Tower)、N 個字元的排列組合。
遞迴
遞迴 (Recursive) 是程式中包含自我呼叫 (self-calling)。
function Recursive(int x){
int y = 0; //y 為區域變數
...
if(x != 0){
Recursive(y);
}
int z = Recursive(y) + 1; //compiler會從這裡開始執行
/*
compiler內部會儲存:
temp = Recursive();
z = temp+1;
*/
}//end敘述
/*問題: 當compiler遇到end敘述時,如何判斷是什麼樣的結束?
(是某次的遞迴結束而已,還是整個程式的結束?)*/
1. 當程式遇到 recursive call 時,必須保存當時的執行狀態;即 push 需要保存的內容到 stack memory 中:
- 參數值 (e.g. x 值)
- 區域/暫存變數值 (e.g. y 值)
- 返回位址 (return address),紀錄遞迴呼叫完成後、下一個可執行的程序是什麼
2. 接下來,go to 程式開端執行
3. 若執行遇到 end 敘述時,則:
if(stack == 空){
整個程式執行結束
}
else{ //stack不為空。即某一次的遞迴結束,而非整個程式執行結束
pop stack; //取出參數,區域變數及返回位址
go to "返回位址" 執行
};
由於 Stack 空間有限,若又不斷 push 的話就會爆掉,造成所謂的「Stack Overflow」:Recursive 所需的 Stack 空間= (每次 push 的量) * (recursive call 次數) 。
另外,Push/Pop 執行的時間即是一個損耗,所以 Recursive 相當花時間。
Recursive 和 Iterative 的比較
目前學者已證明了——任何一個問題的解決方式,必存在 Recursive 和 Iterative 兩種形式;也就是說,解決同一個問題,可以有遞迴和非遞迴的兩種解法。
從遞迴轉換到非遞迴的程式有一個 SOP 流程可以轉換。但從非遞迴到遞迴沒有 SOP 流程,只能從「理論上」知道一定可以成功轉換過去。
舉例來說,計算一個數字的階乘 (Factorial):
n! = 1 * 2 * 3 * ... * n-1 * n, n >= 0 0! = 1
可以有兩種寫法:
int Factorial_iterative(int n){
if(n == 0){
return 1;
}else{
int k = 1;
int i;
for(i = 1; i <= n; i++){
k = k*i;
}
return k;
}
}
int Factorial_recursive(int n){
if(n == 0){
return 1;
}else{
return n*Factorial(n-1);
}
}
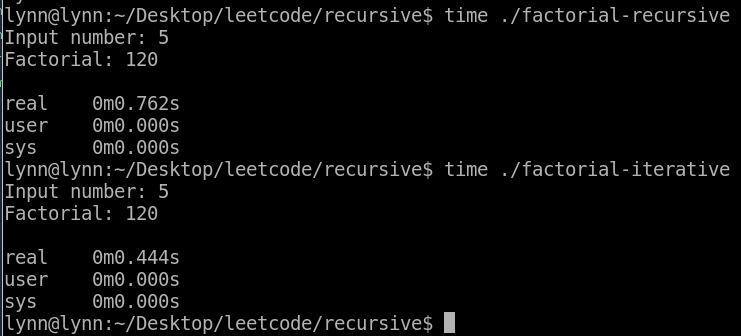
可以看到同樣計算 5! = 120 ,Iterative 版本所需的時間更少。至於兩種方式何種較佳呢?這就牽涉到效能 (空間、時間) 的分析啦!
-
Recursive 的優缺
- 優:程式碼較為精簡
- 優:區域 (暫存) 變數較少
- 優:佔用的儲存空間較少
- 缺:程式執行的時間較長、較無效率
- 缺:需要額外的 Stack 支持
-
Iterative 的優缺
- 優:程式執行的時間較短 (不用額外處理 push/pop)
- 優:不需額外的 Stack 支持
- 缺:程式碼較冗長
- 缺:區域 (暫存) 變數較少
- 缺:佔用的儲存空間較大
經典 RECURSIVE 題型
1. 最大公因數
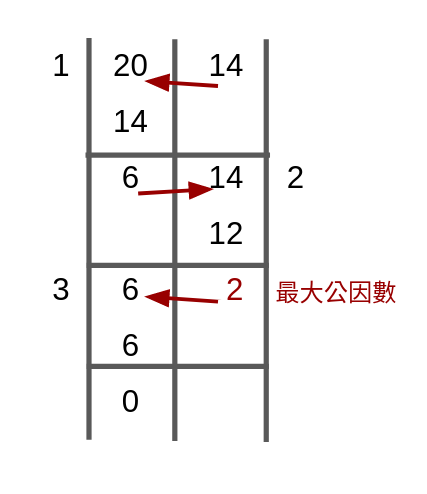
利用輾轉相除法:
#include <stdio.h>
int GCD(int a, int b){
if(a%b == 0){
return b;
}else{
return GCD(b, a%b);
}
}
int main(){
printf("Input two numbers: ");
int a, b;
scanf(" %d %d", &a, &b);
int result = GCD(a, b);
printf("GCD result: %d\n", result);
}
2. FIBONACCI 數列
一個有名的數列 Fibonacci 數列定義如下:
這個數列在 13 世紀初由義大利比薩 (Pisa) 一位叫李奧納多 (Leonardo) 的人所提出:
- 小兔出生後兩個月就能長成大兔,可以生小兔。
- 可生育的大兔子每個月可以生一對小兔,而且剛好是雄雌各一。
- 兔子永生不死。
首幾個 Fibonacci 數是:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……
RECURSIVE VERSION
int Fibo(int n){
if(n == 0){
return 0;
}else if(n == 1){
return 1;
}else{
return Fibo(n-1)+Fibo(n-2);
}
}
//Time: 近似於O(2^n)
ITERATIVE VERSION
int Fibo(int n){
if(n == 0){
return 0;
}else if(n == 1){
return 1;
}else{
int a = 0;
int b = 1;
int i, c;
for(i = 1; i < n; i++){
c = a + b;
a = b;
b = c;
}
return c;
}
}
//Time: O(n)
DP (DYNAMIC PROGRAMMING) VERSION
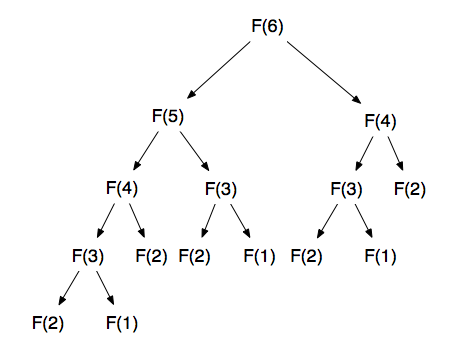
在計算 Recursive 題目時,會有蠻多重複的計算,比如在計算 F(4) 時得算出 F(3) / F(2) / F(1) /F(0),但計算 F(3) 時又另外把 F(2) / F(1) /F(0) 重複計算…。
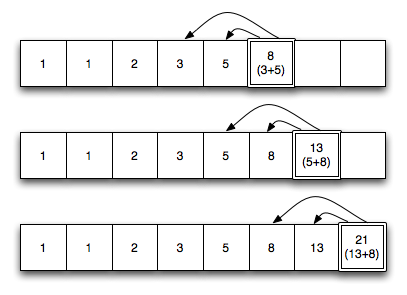
因此我們使用 Dynamic Programming 的技巧來求 Fibonacci 數列,也就是使用一個一維陣列來儲存之前計算過的成果。
int Fibo(int n){
int F[n+1];
F[0] = 0;
F[1] = 1;
if(n < 2){
return F[n];
}else{
int i;
for(i = 2; i <= n; i++){
F[i] = F[i-1] + F[i-2]; //保存先前的運算成果
}
return F[n];
}
}
//Time: o(n)
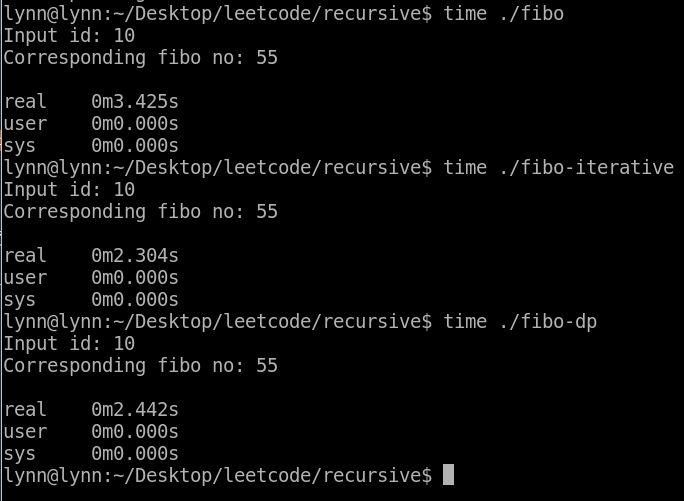
可以發現相同的結果:F(10) = 55,Recursive、Iterative、Dynamic Programming 三個版本的時間差異是由大到小。
遞迴的 Fibonacci 數列的時間會這麼長,原因是因為先前算過的內容得重新再算一次、太多冗餘的計算。如果改成 Iterative 版本或 DP 版本就會更有效率。
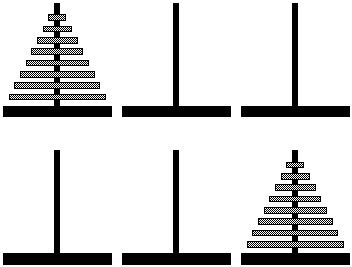
3. 河內塔問題
欲將 A 柱上的 n 個盤子搬移到 C 柱,但必須遵守以下規則:每次只能移動一個圓盤,且大盤不能疊在小盤之上。
#include <stdio.h>
int count = 0;
void hanoi(int n, char A, char B, char C)
{
if (n == 1)
{
printf("%d: 將第 %d 個圓盤由 %c 移到 %c\n", count++, n, A, C);
}
else
{
hanoi(n - 1, A, C, B);
printf("%d: 將第 %d 個圓盤由 %c 移到 %c\n", count++, n, A, C);
hanoi(n - 1, B, A, C);
}
}
int main()
{
int n;
printf("請輸入河內塔的高度:");
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
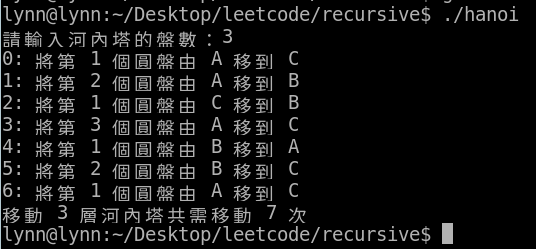
printf("移動 %d 層河內塔共需移動 %d 次\n", n, count);
return 0;
}
遞迴關係式:T(n) = T(n-1) + T(1) + T(n-1),且 T(1) = 1 ;則 T(n) = 2*T(n-1) + T(1) ,解出 T(n) 為 2^n -1。
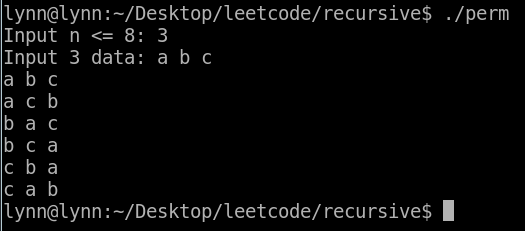
4. 列印 n 個字元的排列組合 (Permutations)
a, b, c ------- abc acb bac bca cba cab => Perm(a, b, c) 可拆解為 'a' + Perm(b, c) 'b' + Perm(a, c) 'c' + Perm(b, a)
//main function呼叫:Perm(list, 1, n)
void Perm(char list[], int i, int n){ //list[i] ~ list[n] permutation
int j;
if(i == n){
for (j = 1; j <= n; j++){
printf("%c ", list[j]);
}
printf("\n");
}
else{ //i < n
for(j = i; j <= n; j++){
swap(&list[i], &list[j]); //list[j] as head
Perm(list, i+1, n); //list[i+1] ~ list[n] permutation
swap(&list[i], &list[j]); //return to the original list
}
}
}