希爾排序 (Shell Sort)

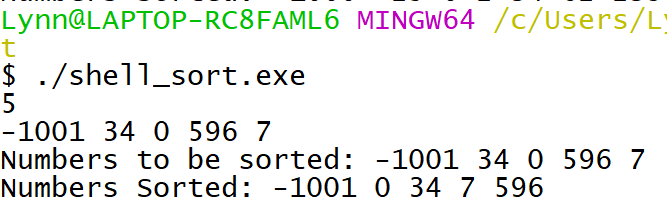
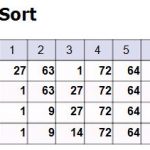
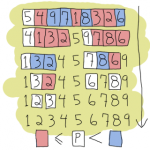
希爾排序法 (Shell Sort) 是插入排序法 (Insertion Sort) 的改良版，因為簡單、效率不錯，在實際應用上的接受度頗高。

Insertion Sort 在資料幾乎已經排序好的情況下，時間複雜度越接近 O(n)。也就是說，Shell Sort 是基於插入排序的以下兩點性質而提出改進方法的：

•  Insertion Sort 在對幾乎已經排好序的資料操作時，效率高，即可以達到線性排序的效率
• 但 Insertion Sort 一般來說是低效率的，因為每次只能將資料移動一位

Shell Sort 提出的概念是──將整個陣列依照預先指定的間隔長度 d，交錯分割成數個小陣列，並以插入排序的方式將這些小陣列個別排序，然後逐漸縮小間隔長度 d ，直到 d 等於 1。

此時再作最後一次插入排序。

步驟

• 由大到小選定數個間距 (span)
• for i = 1 to (n-span) do
  • 將資料依指定的 span 分組，進行插入排序──比較第 i 筆與第 i+span 筆資料，若前者大於後者，則交換前後資料
  • 每一回合必須持續做到沒有交換 (No SWAP) 和 span 為 1 為止，才可結束本回合進入下一回合
• 回合數是由 span 的型式所決定

若某回合的 span 值為 k，則表示有 k 個小陣列要排序好，每個小陣列的資料量大約是 n/k 。

常見的 Span 型式

1. 

n = 10
-----------------
Pass 1: span = 5
Pass 2: span = 2
Pass 3: span = 1

2.

Pass 1: span = 15 = 2^4-1
Pass 2: span = 7 = 2^3-1
Pass 3: span = 3 = 2^2-1
Pass 4: span = 1 = 2^1-1

 

虛擬碼

ShellSort(A[], n)
  span = n/2
  while (span>-1) do
  repeat
  flag = 0 //有無swap發生?
  for i = 1 to (n-span) do
  if(A[i] > A[i+1]) then
    swap(A[i] > A[i+span])
    flag = 1
  until (flag == 0) //持續做到沒有交換為止
  span = span/2 //下一個回合的span

 

程式碼

void swap(int *a, int *b){
  int temp;
  temp = *a;
  *a = *b;
  *b= temp;
};

int shell_sort(int A[], int n){
  int span, i;
  span = n/2;
  while(span>=1){
    for(i = 0; i<(n-span); i++){
      if(A[i]>A[i+span]){
        swap(&A[i], &A[i+span]);
      }
    }
    span = span/2;
  }
};

int main(){
  int count, i;
  scanf("%d", &count);
  int list[count];
  printf("Numbers to be sorted: ");
  for(i = 0; i<count; i++){
    scanf("%d", &list[i]);
    printf("%d ", list[i]);
  }
  printf("\n");
  shell_sort(list, count);
  printf("Numbers Sorted: ");
  for(i = 0; i<count; i++){
    printf("%d ", list[i]);
  }
  return 0;
}

 

時間複雜度

1. Worst Case: O(n²)

2. Average: O(n²)

2. Best Case: 到目前為止尚無定論，與 Span 的型式有關。可能有 O(n^3/2)、O(n^3/4)、O(n^7/6)

 

空間複雜度：o(1)

需要一個額外的空間，紀錄目前欲插入的資料，即暫存用來交換的 temp 變數。

 

穩定性：Unstable

Pass 0
--------------------------------- 
array index: [0] [1] [2] [3]
input data:   5   5*  3   8

Pass 1: Span = 2
--------------------------------- 
array index: [0] [1] [2] [3]
input data:   3   5*  5   8

可以發現 5 和 5* 在中間過程中交換了，可知為 Unstable Sorting。