泡泡排序 (Bubble Sort)

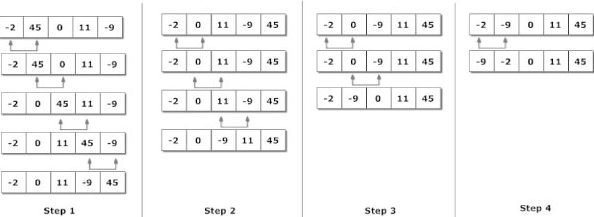
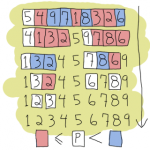
由左而右、兩兩比較相鄰資料，若前者大於後者，則將兩者交換來完成排序。當資料個數為 n 時，比較過程將分成 n-1 回合。

第 i 回合會將第 i 大的資料像泡泡一樣浮現在由右數回來的第 i 個位置。

比如 A[4] = {2, 4, 7, 3}，第 1 回合要把第 1 大的數字 7 排序：

Pass 1: 4, 2, 7, 3
Pass 2: 2, 4, 7, 3
Pass 3: 2, 4, 7, 3
Pass 4: 2, 4, 3, 7

如果某回合過程中完全沒有發生交換，則代表排序完成，後面回合也無須再進行。

虛擬碼

BubbleSort(A, n) //排序A[1]到A[n]
  for i = 1 to (n-1) do
    flag = 0 //表示有無交換發生
    for j = 1 to (n-i) do
      if A[j] > A[j+1] then
        swap A[j] and A[j+1]
        flag = 1
      end if
      if(flag == 0) then Exit;
    end for
  end for

 

程式碼

#include <stdio.h>

void swap(int *a, int *b){
  int temp;
  temp = *a;
  *a = *b;
  *b= temp;
}

int bubble_sort(int A[], int n){
  int i, j, flag;
  for(i = 0; i<n-1; i++){ //n個數字排序，只用 n-1 回
    int flag = 0; //表示有無發生交換
    for(j = 0; j < n-i; j++){ //從第一個數字開始比較，直到最後一個數字
      if(A[j]>A[j+1]){
        swap(&A[j], &A[j+1]);
        flag = 1;
      }
    }
    if(flag == 0) break; //此回合沒有發生交換
  }
}

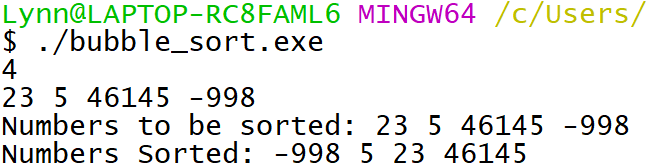
int main(){
  int count, i;
  scanf("%d", &count);
  int list[count];
  printf("Numbers to be sorted: ");
  for(i = 0; i<count; i++){
    scanf("%d", &list[i]);
    printf("%d ", list[i]);
  }
  printf("\n");
  bubble_sort(list, count);
  printf("Numbers Sorted: ");
  for(i = 0; i<count; i++){
    printf("%d ", list[i]);
  }
  return 0;
}

 

時間複雜度

1. Best Case: O(n)

input data 恰好由小到大呈現

input: 1, 2, 3, ..., n-1, n
Pass 1: 經過 (n-1) 次比較後，發現無任何交換發生，排序完成。

=>O(n)

 

2. Worst Case: O(n²)

input data 反序由大到小呈現。

input: n, n-1, n-2, ... , 2, 1                交換次數
------------------------------------------------------
Pass 1: (n-1), (n), n-2, ... , 1, n            n-1 次
Pass 2: (n-2), (n-3), ... , 1, n-1, n          n-2 次
Pass 3: (n-3), (n-4), ... , 1, n-2, n-1, n     n-3 次
...
Pass (n-1): 1, 2, ..., n-1, n                    1 次
 
Total = (n-1)+(n-2)+ ... +1 
      = n(n-1)/2 次
=>O(n^2)

改用 Recursive Time Function 來解：

T(n) = (n-1) + T(n-1), T(1) = 0  //O(n) 為Pass 1 之平均交換時間
= T(n-2) + (n-2) + (n-1)
= T(n-2) + c*((n-1)+n)
= ...
= T(1) + 1 + 2 + ... + (n-1)
= n(n-1)/2

=>O(n^2)

 

3. Average Case: O(n²)

T(n) = O(n) + T(n-1), T(1) = 0  //O(n) 為Pass 1 之平均交換時間

T(n) 
= T(n-1) + c*n, c 為正常數
= T(n-2) + c*((n-1)+n)
= ...
= T(1) + c*(2+ ... + n)
= c* (n+2)(n-1)/2

=>O(n^2)

 

空間複雜度: O(1)

需要一個額外的空間儲存 temp 變數來做交換。

 

穩定性: Stable

input data: ..., 5, 5*, ...
Pass 1: ..., 5, 5*, ...

由於 5 並不大於 5*，交換不發生、仍維持原順序，故為 Stable Sorting。