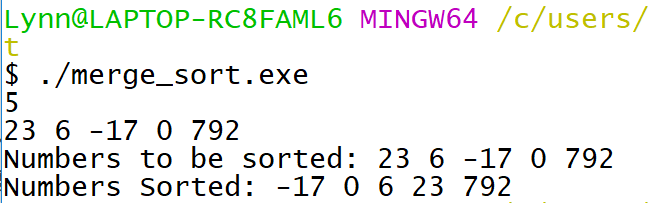
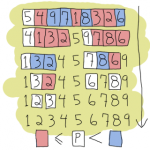
本篇將為大家介紹合併排序 (Merge Sort) 的原理、虛擬碼、程式碼與時間/空間複雜度分析。
合併排序
是外部排序 (External Sorting) 常用的排序方法之一,採用 “Divide-and-Conquer” 策略。
Devide-and-Conquer 步驟:
- Devide: 將原問題分成若干個仔問題
- Conquer: 遞迴解決各個子問題;當子問題夠小時則直接解
- Combine: 將子問題的解合併成原問題的解
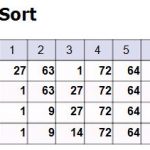
Merge Sort 是 Devide-and-Conquer 相當著名的應用之一,步驟如下:
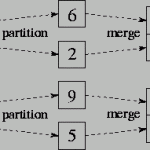
- 將原本的 Data List 切割成兩等分
- 將左、右的 Sublist 各自以 Merge Sort 排序
- 合併左右半部的兩個 Sublist 成為一個新的 Data List
虛擬碼 (Pseudo Code)
Merge(arr_1[], arr_2[]){
p 為 arr_1[]的起始 index;
q 為 arr_2[]的起始 index;
while(arr_1 && arr_2 尚未scan完畢){
if (p.data < q.data) then{
p.data 先輸出到一個新的 array;
p = p + 1;
}
else{
q.data 先輸出到一個新的 array;
q = q + 1;
}
while(arr_1尚未scan完畢){
複製 arr_1 剩下的 data 到新的 array 裡;
}
while(arr_2尚未scan完畢){
複製 arr_2 剩下的 data 到新的 array 裡;
}
}
}
MergeSort(A[], head, tail){
if(head < tail){
mid = (head + tail) / 2;
MergeSort(arr, head, mid);
MergeSort(arr, mid+1, tail);
Merge(arr, head, mid, tail);
}
}
程式碼
#include <stdio.h>
#include <stdlib.h>
// Merge two subarrays of A[].
// First subarray is arr[head..mid]
// Second subarray is arr[mid+1..tail]
void merge(int arr[], int head, int mid, int tail){
int lenA = mid - head + 1;
int lenB = tail - (mid + 1) + 1;
int A[lenA];
int B[lenB];
//Copy data to temp arrays A[] and B[]
int i, j, k;
for(i = 0; i < lenA; i++){
A[i] = arr[head + i];
}
for(j = 0; j < lenB; j++){
B[j] = arr[mid + 1 + j];
}
// Merge two temp arrays back into arr[head..tail]
i = 0;
j = 0;
k = head;
//while array A and B haven't finished scanning
while(i < lenA && j < lenB){
if(A[i] < B[j]){
arr[k] = A[i];
i++;
}
else{
arr[k] = B[j];
j++;
}
k++;
}
//Copy the remaing elements into arr[], if A[] haven't finished scanning
while(i < lenA){
arr[k] = A[i];
i++;
k++;
}
//Copy the remaing elements into arr[], if B[] haven't finished scanning
while(j < lenB){
arr[k] = B[j];
j++;
k++;
}
}
void merge_sort(int arr[], int head, int tail){
if(head < tail){
int mid = (head + tail) / 2;
merge_sort(arr, head, mid);
merge_sort(arr, mid+1, tail);
merge(arr, head, mid, tail);
}
}
int main(){
int count, i;
scanf("%d", &count);
int list[count];
printf("Numbers to be sorted: ");
for(i = 0; i<count; i++){
scanf("%d", &list[i]);
printf("%d ", list[i]);
}
printf("\n");
merge_sort(list, 0, count-1);
printf("Numbers Sorted: ");
for(i = 0; i<count; i++){
printf("%d ", list[i]);
}
return 0;
}
時間複雜度 (Time complexity)
如果 Sublist A 的長度為 m、Sublist B 的長度為 n,則合併兩個 Sublist:
- 最少比較次數 = m 或 n (若將 A 長度改為 n,則為 n)
- 最多比較次數 = m + n – 1 次 (若將 A 長度改為 n,則為 2n-1)
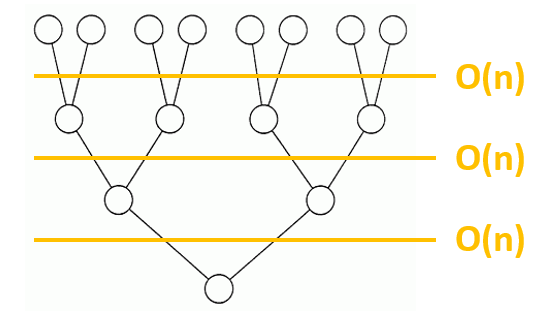
=> 時間皆為 O(n)
已知每回合 merge 所花費的時間為 O(n),則 n 個 Data 做 Merge Sort 需要幾個回合?
由於 Merge Sort 過程相當於一棵 Binary Tree,故 Merge Sort 的回合數相當於「Binary Tree 的高度 – 1」。
n 個 Data 的 Binary Tree 高度為 log2 n + 1,故回合數為 log2 n。
- Merge Sort 的總時間
- = 回合數 * 每回合所花的時間
- = log n * O(n)
- = O(n logn)
Average/Best/Worst Case 的時間皆為 O(n logn)。
改用 Recursive Time Function 運算仍可得相同結果:
T(n) = T(n/2) + T(n/2) + c*n //c為正常數, c*n為合併的時間 = 2*T(n/2) + c*n => T(n) = O(n logn)
空間複雜度 (Space Complexity)
需要一個與原來 Data List 一樣的額外空間,來暫時儲存每一回合的合併結果,故為 O(n)。
穩定性:Stable
array A | array B
5 , 8 | 5* , 10
merge
5 , 5* , 8 , 10
可知 5 和 5* 的位置在合併後仍不會前後交換。