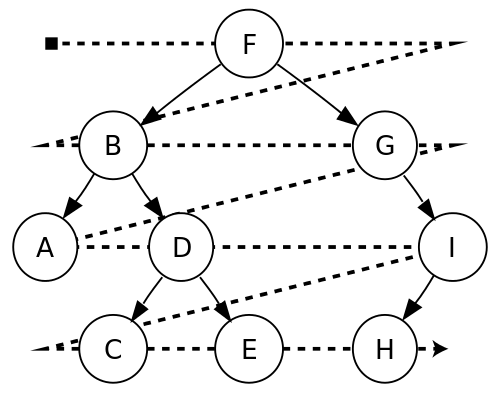
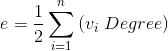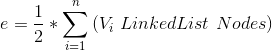圖形的表示
圖形的表示有兩種方法:相鄰矩陣 (Adjacency Matrix) 與相鄰串列 (Adjacency List)。
相鄰矩陣 Adjacency Matrix
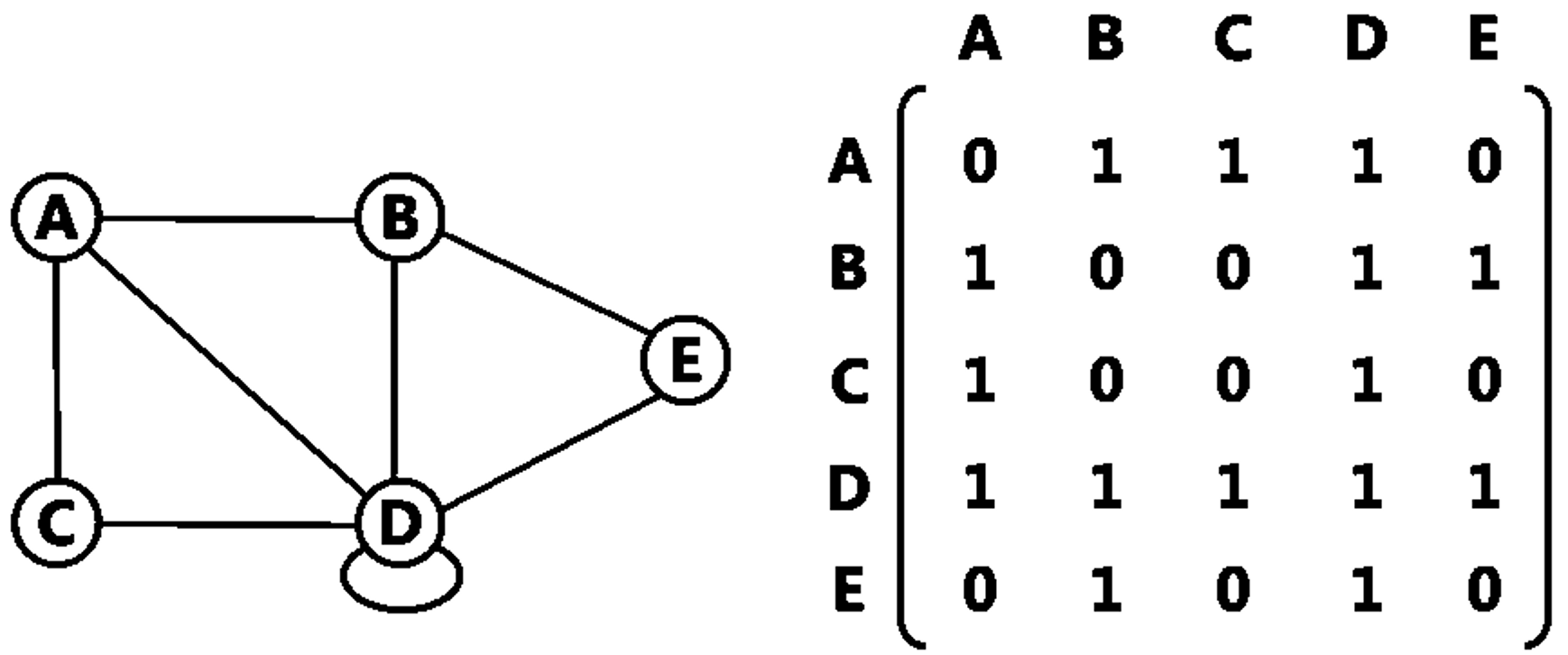
(1) 無向圖
對一個頂點數為 n 的圖形,準備一個 nxn 矩陣 A,其中:
A[i, j] = 1, if (i, j)邊存在 A[i, j] = 0, if (i, j)邊不存在
觀察上圖可知:
- 由於 D 與自己形成迴圈,所以此對角線不全為 0。然而若此圖為 Simple Graph、頂點不能與自己形成迴圈,則對角線元素均為 0。
- 此為無向圖,相鄰矩陣為對稱矩陣 (Symmetric Matrix)。由於邊 (Vi, Vj) 存在時、A[i, j] 與 A[j, i] 的值均為 1。為了節省記憶體,可以只儲存相鄰矩陣的上半部或下半部,即上三角矩陣或下三角矩陣。
- 第一行加總與第一列加總會相等、為點 A 的分支度,第二行與第二列加總會相等、為點 B 的分支度… 以此類推。
Q1: 判斷邊 (i, j) 是否存在?
if A[i, j] = 1 then 存在 else 不存在
Time: O(1)
Q2: 求頂點 i 之 degree?
- 第 i 列或第 i 行元素加總即可
Time: O(n)
Q3: 求圖形邊數?
- 邊數 = (所有元素加總 = 所有點的 Degree)÷2
Time: O(n2)
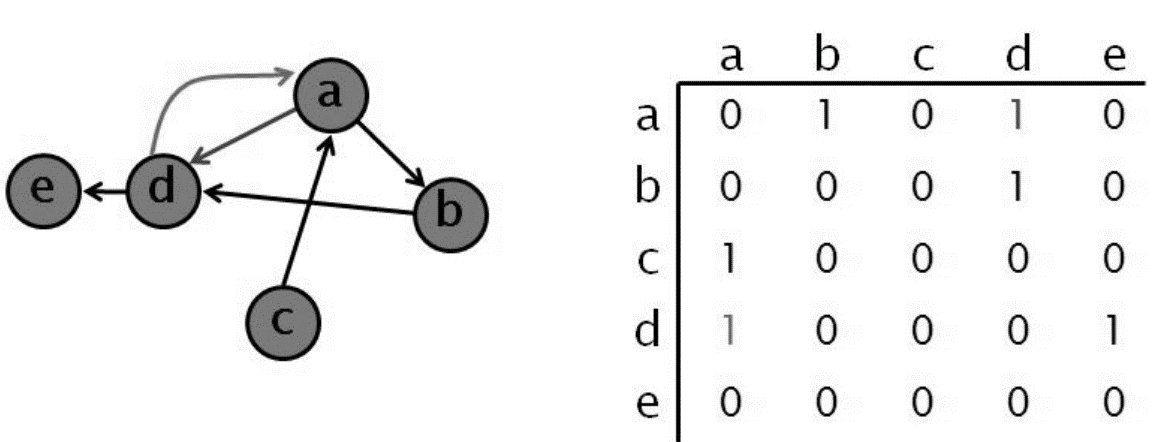
(2) 有向圖
觀察上圖可知:
- 此圖為 Simple Graph、頂點不能與自己形成迴圈,則對角線元素均為 0。
- 有向圖的相鄰矩陣未必為對稱矩陣 (Symmetric Matrix)。由於邊 (Vi, Vj) 存在時、不代表 (Vi, Vj) 會同時存在。
- 第一列加總為點 A 的分支度,第二列加總為點 B 的分支度… 以此類推。
Q1: 判斷邊 (i, j) 是否存在?
if A[i, j] = 1 then 存在 else 不存在
Time: O(1)
Q2: 求頂點 i 之 Out-degree 或 In-degree?
- 第 i 列元素加總 = Out-degree
- 第 i 行元素加總 = In-degree
Time: O(n)
Q3: 求圖形邊數?
- 所有頂點的 Out-degree 加總
Time: O(n2)
(3) 相鄰矩陣的優缺
優點:
- 適合儲存邊數非常多的圖形。
- 適合經常要判斷邊是否存在的問題,複雜度僅 O(1)。
缺點:
- 當圖形上的頂點數很多、邊數很少時,會形成稀疏矩陣 (sparse matrix),浪費記憶體空間。
- 求圖形上的邊數、判斷是否為連通圖、判斷有無Cycle形成,都需要 O(n2) 時間。
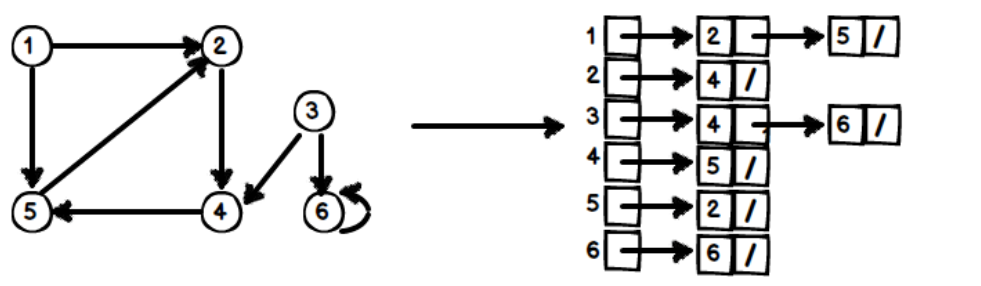
相鄰串列 Adjacency LIst
G = (V, E),|V| = n、|E| = e。若圖形包含 n 個頂點,則使用 n 個 Linked Lis存放該圖形,每個 Linked List 都代表一個頂點、和與其相鄰的頂點。
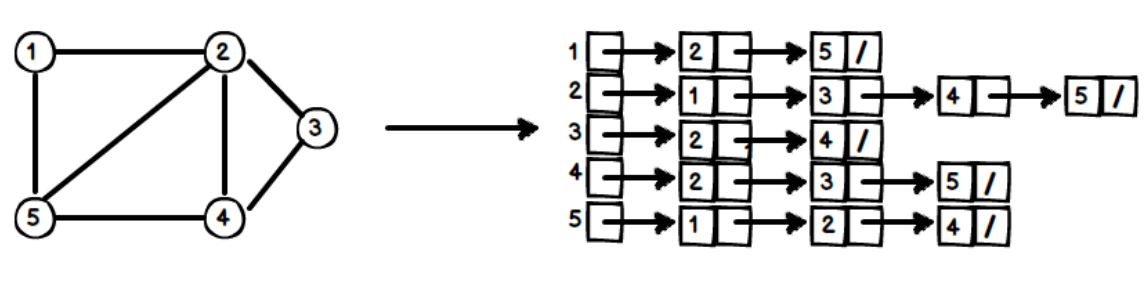
(1) 無向圖
Q1: 判斷邊 (i, j) 是否存在?
- 檢查 Vi 的鏈結串列中是否有 j Node 存在。
Time: O(Vi串列長度) ≤ O(所有Node數) = O(e)
Q2: 求頂點 i 之 Degree?
- 求 Vi 串列長度
Time: O(Vi串列長度)
Q3: 求圖形邊數?
- Vi LinkedList Nodes 意即 Vi 的串列長度、Vi 串列的 Node 總數。
Time: O(n+e)
問:為何不是 O(n*e)?
s = 0;
for i = 1 to n do //連同失敗、跑n+1次: O(n) Time
{
while(Vi 串列尚未scan完畢) //Node總數,和邊數e成正比
{
s++; //O(e)
}
}
e = s/2; //1次
-> Time: O(n+e)
(2) 有向圖
Q1: 判斷邊 (i, j) 是否存在?
- 檢查 Vi 的鏈結串列中是否有 j Node 存在。
Time: O(Vi串列長度) ≤ O(所有Node數) = O(e)
Q2: 求頂點 i 之 Out-degree 與 In-degree?
- 求 Vi 串列長度 = Out-degree
- 檢視所有串列,找出 i Node的出現次數 = In-degree
Time: O(n+e)
Q3: 求圖形邊數?
- Vi LinkedList Nodes 意即 Vi 的串列長度、Vi 串列的 Node 總數。
Time: O(n+e)
s = 0;
for i = 1 to n do //連同失敗、跑n+1次: O(n) Time
{
while(Vi 串列尚未scan完畢) //Node總數,和邊數e成正比
{
s++; //O(e)
}
}
e = s; //1次
-> Time: O(n+e)
(3) 相鄰矩陣的優缺
優點:
- 適合儲存頂點數多、但邊數很少的圖形。
- 能較彈性地使用記憶體,但實作較為複雜。
- 求圖形上的邊數、判斷是否為連通圖、判斷有無Cycle形成,僅需 O(n+e) 時間。
- (假設圖形的頂點個數 n、邊數 e。用相鄰串列存放無向圖時, 作為 LinkedList head 的 headnode 有 n 個、Node數有 2e 個;存放有向圖時,headnode 數有 n 個、Node 數有 e 個,因此圖形的運算時間皆為 O(n+e) )
缺點:
- 經常要判斷邊是否存在的問題,複雜度為 O(e)。
- 求圖形上的邊數、判斷是否為連通圖、判斷有無Cycle形成,都需要 O(n2) 時間。
實作相鄰串列的程式碼
這邊我們利用 C++ STL 的 deque 功能來建立可以前後增加刪除的陣列。
#include <stdio.h>
#include <deque>
using namespace std;
class GraphNode{
public:
int id;
deque<int>adjacency;
int discovered;
GraphNode(int _id){
id = _id;
discovered = 0;
}
void dump(){
printf("Vertex: %d, I'm adjacent to: ", id);
int i;
for(i = 0; i<adjacency.size(); i++){
printf("%d ", adjacency[i]);
}
printf("\n");
}
};
deque<GraphNode*> NodeList;
int main(){
int node_count, edge_count;
printf("Enter no of vertices: ");
scanf(" %d", &node_count);
printf("Enter no of edges: ");
scanf(" %d", &edge_count);
int i, j;
for(i = 0; i<node_count; i++){
NodeList.push_back( new GraphNode(i) );
}
printf("Enter %d pairs of verteices: \n", edge_count);
for( j = 0; j < edge_count; j++ ){
int node_1, node_2;
scanf("%d %d", &node_1, &node_2);
NodeList[node_1]->adjacency.push_back(node_2);
NodeList[node_2]->adjacency.push_back(node_1);
}
for( i = 0; i < NodeList.size(); i++ ){
NodeList[i]->dump();
}
return 0;
}
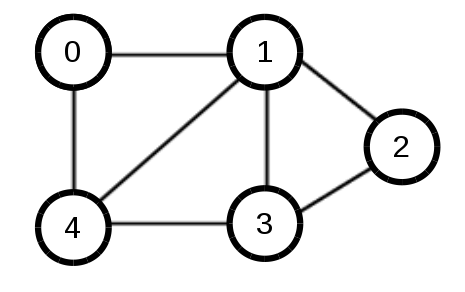
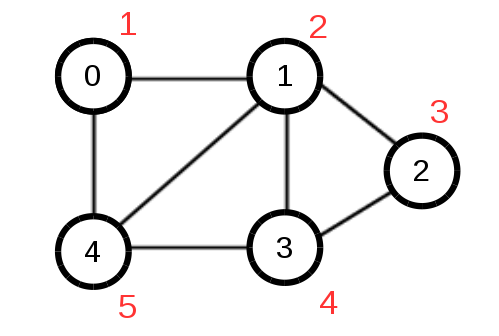
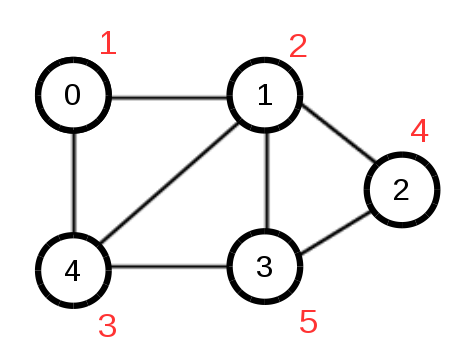
實作範例圖:
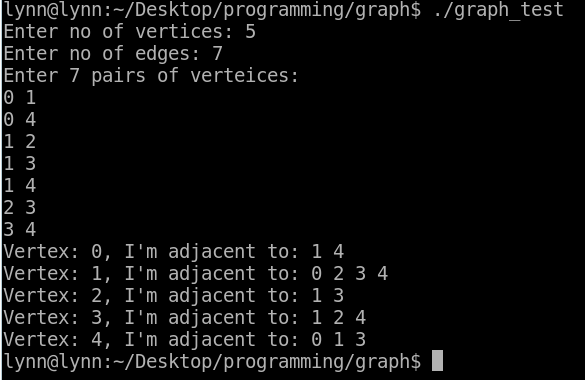
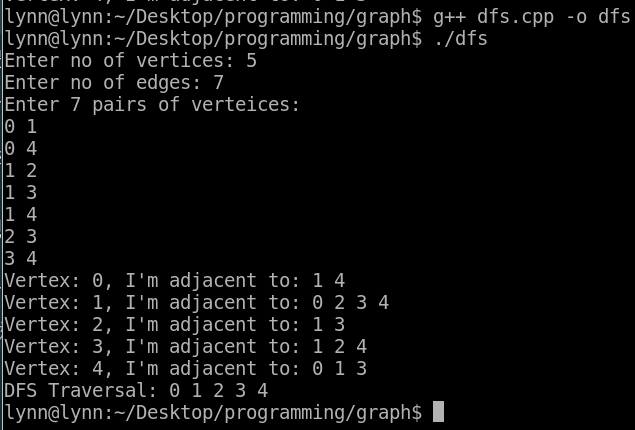
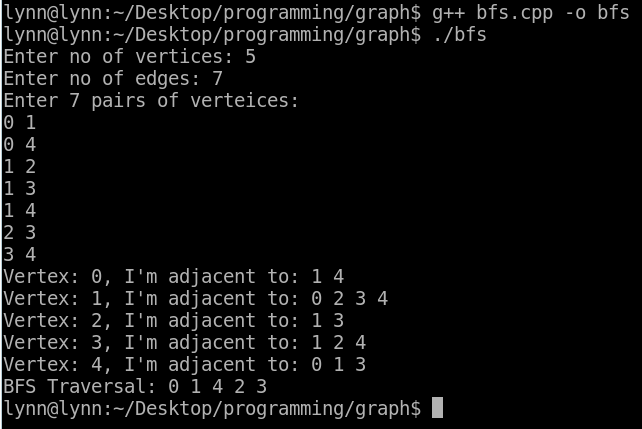
結果:
圖形走訪(Graph Traversal)
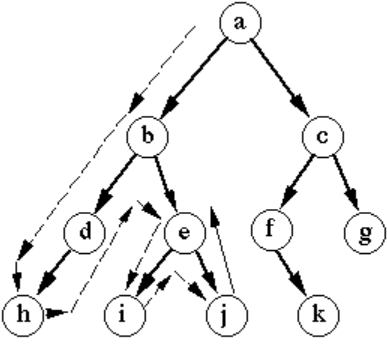
深度優先搜尋 DFS (Depth First Search)
DFS 就像試探著走迷宮,從起點開始、任意選一點與起點相鄰的點行走,行走過的點會被標記起來;再將下一個點視為起點、繼續選擇與該點相鄰的點行走… 直到發現所有的點都已被標記過,即相鄰此點的所有點都已經走過了,則退回上一個分叉路口,繼續探訪。
直到所有的點都被標記過了,則搜索完畢。
虛擬碼 (ds版)
DFS(V:起點)
visited[V] = TRUE;
for each vertex W adjacent to V do
if (not visited[W]) then
DFS(W);
end if
end for
虛擬碼 (Algo版)
- u.color = 頂點 u 的顏色
- White: 尚未拜訪過 (undiscovered)
- Gray: 若 u 為 discovered,但 u 的相鄰點 v 為 undiscovered
- Black: 結束 u 與其所有相鄰點的拜訪
- u.d = 起點 s 到 u 點的距離 ( = 邊數 = 路徑長)
- u.π = u 的父點 (意即從哪個點連到 u)
DFS(G){
for each vertex u in G //設初始值, Time: O(V)
{
u.color = White; //所有點設為白色
u.π = Nil; //所有點的父點皆未知
}
time = 0;
for each vertex u in G //Time: O(V)
{
if (u.color==White) then
{
DFS-Visit(G,u);
}
}
}
DFS-Visit(G, u){
time = time+1;
u.d = time; //u首度被discovered之time
u.color = Gray; //被拜訪,尚未結束
for each vertex v in G.adj[u]
{
if(v.color==White) then
{
v.π = u;
DFS-Visit(G, V);
}
}
u.color = Black; //u已結束
time = time+1;
u.f = time; //u的finished time
}
=>Time = O(V+E)
程式碼
#include <stdio.h>
#include <deque>
using namespace std;
class GraphNode{
public:
int id;
deque<int>adjacency;
int discovered;
GraphNode(int _id){
id = _id;
discovered = 0;
}
void dump(){
printf("Vertex: %d, I'm adjacent to: ", id);
int i;
for(i = 0; i<adjacency.size(); i++){
printf("%d ", adjacency[i]);
}
printf("\n");
};
};
deque<GraphNode*> NodeList;
void DFS(int vertex){
GraphNode* curr = NodeList[vertex];
curr->discovered = 1;
printf("%d ", vertex);
int i, next;
for( i = 0; i < curr->adjacency.size(); i++){
next = curr->adjacency[i];
if(NodeList[next]->discovered == 0){
DFS(next);
}
}
}
int main(){
int node_count, edge_count;
printf("Enter no of vertices: ");
scanf(" %d", &node_count);
printf("Enter no of edges: ");
scanf(" %d", &edge_count);
int i, j;
for(i = 0; i<node_count; i++){
NodeList.push_back( new GraphNode(i) );
}
printf("Enter %d pairs of verteices: \n", edge_count);
for( j = 0; j < edge_count; j++ ){
int node_1, node_2;
scanf("%d %d", &node_1, &node_2);
NodeList[node_1]->adjacency.push_back(node_2);
NodeList[node_2]->adjacency.push_back(node_1);
}
for( i = 0; i < NodeList.size(); i++ ){
NodeList[i]->dump();
}
printf("DFS Traversal: ");
DFS(0);
printf("\n");
return 0;
}
實作範例圖:
結果:
廣度優先走訪 BFS (Breadth First Search)
BFS 以某個頂點作為起始點,一開始拜訪該頂點、再接著拜訪該頂點的所有相鄰頂點,接下來再拜訪下一層的頂點,直到所有的頂點皆拜訪過為止。
虛擬碼 (DS 版)
BFS(V:起點)
//Assume visited[1..n]
visited[V] = TRUE;
Create(Q);
Enqueue(Q, V);
while(not Isempty(Q)) do
u = Dequeue(Q);
for each vertex w adjacent to u do{
for each vertex W adjacent to V do
if (not visited[W]) then
DFS(W);
虛擬碼 (ALGO版)
- u.color = 表示頂點 u 的顏色
- White: 尚未拜訪 (undiscover)
- Gray: 若 u 為 discovered,但 u 的相鄰點 v 為 undiscovered
- Black: 結束 u 與其所有相鄰點的拜訪
- u.d = 起點 s 到 u 點的距離 ( = 邊數 = 路徑長)
- u.π = u 的父點 (意即從哪個點連到 u)
除了頂點的資料結構之外,還需要一個 queue 來管理灰色的頂點,代號 Q。
BFS(G, s){ //s為起點
for each vertex u in G-{s} //初始值設定, Time: O(V)
{
u.color = white; //將起點以外的所有點設為白色
u.d = ∞;
u.π = Nil; //父點皆未知
}
//拜訪起點
s.color = Gray;
s.d = 0;
s.π = Nil;
//建立空佇列 Q
CreateQ(Q);
//將起點s加入Q
Enqueue(Q, s);
//Q不為空時
while(not IsEmpty(Q)) do
{
u = Dequeue(Q); //O(1)*V次, Time: O(V)
for each v in G.adj[u] do //Time: O(E)
{
if (v.color == White) then
{
v.color = Gray;
v.d = u.d+1;
v.π = u;
Enqueue(Q, v);
}
}
u.color = Black;
}
}
=> O(V)+O(V)+O(E) = O(V+E)
程式碼
#include <stdio.h>
#include <deque>
using namespace std;
class GraphNode{
public:
int id;
deque<int>adjacency;
int discovered;
GraphNode(int _id){
id = _id;
discovered = 0;
}
void dump(){
printf("Vertex: %d, I'm adjacent to: ", id);
int i;
for(i = 0; i<adjacency.size(); i++){
printf("%d ", adjacency[i]);
}
printf("\n");
};
};
deque<GraphNode*> NodeList;
void BFS(int start){
deque<int> que;
que.push_back(start);
NodeList[start]->discovered = 1;
int curr_id, adj_id;
GraphNode* curr_node;
GraphNode* adj_node;
while(que.size() != 0){
curr_id = que[0];
que.pop_front();
printf("%d ", curr_id);
curr_node = NodeList[curr_id];
for(int i = 0; i < curr_node->adjacency.size(); i++){
adj_id = curr_node->adjacency[i];
adj_node = NodeList[adj_id];
if(adj_node->discovered == 0){
adj_node->discovered = 1;
que.push_back(adj_id);
}
}
}
}
int main(){
int node_count, edge_count;
printf("Enter no of vertices: ");
scanf(" %d", &node_count);
printf("Enter no of edges: ");
scanf(" %d", &edge_count);
int i, j;
for(i = 0; i<node_count; i++){
NodeList.push_back( new GraphNode(i) );
}
printf("Enter %d pairs of verteices: \n", edge_count);
for( j = 0; j < edge_count; j++ ){
int node_1, node_2;
scanf("%d %d", &node_1, &node_2);
NodeList[node_1]->adjacency.push_back(node_2);
NodeList[node_2]->adjacency.push_back(node_1);
}
for( i = 0; i < NodeList.size(); i++ ){
NodeList[i]->dump();
}
printf("BFS Traversal: ");
BFS(0);
printf("\n");
return 0;
}
實作範例圖:
結果: